70.03 Medios de Representación "A" - Trabajo Práctico - Empalmes
Período: 1er Cuatrimestre 2007
Alumno: García Mendive, Iñaki
Lámina
Datos: (ver hoja de datos)
Recomendación para hacer el trazado definitivo en esta lámina: a los fines de lograr un trazado definitivo del mismo tono y grosor en toda la lámina, conviene priorizar ciertos elementos sobre otros. Por empezar, en las circunferencias resulta más difícil lograr un trazado uniforme que en las rectas. Por ello, siempre conviene trazar primero las circunferencias, y una vez que éstas han sido bien delineadas, proceder a trazar las rectas. En cuanto a cuáles circunferencias trazar primero y cuáles después, no es indistinto: resultan particularmente difíciles las circunferencias de radios menores, por ello es juicioso trazarlas primero a éstas que a las de radios mayores.
Resolución:
- Tangentes a una circunferencia: tenemos el punto
 , y a una distancia
, y a una distancia 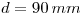 de él, el punto
de él, el punto  , centro de una circunferencia
, centro de una circunferencia  de radio
de radio 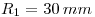 . Para encontrar las tangentes a esta circunferencia por
. Para encontrar las tangentes a esta circunferencia por  debemos trazar otra circunferencia
debemos trazar otra circunferencia  , de radio
, de radio  cuyo centro es el punto medio del segmento
cuyo centro es el punto medio del segmento  . Los puntos
. Los puntos 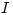 y
y  donde ambas circunferencias se cortan son los puntos de tangencia que buscábamos. Por cada uno de ellos, y por
donde ambas circunferencias se cortan son los puntos de tangencia que buscábamos. Por cada uno de ellos, y por  , trazamos las dos tangentes que necesitábamos.
, trazamos las dos tangentes que necesitábamos.
Este método se justifica por el teorema del arco capaz, también conocido como el teorema del ángulo inscrito o teorema de tales. Sucintamente, y a los efectos prácticos de este ejercicio, el teorema dice: dados dos puntos ( y
y  ) diametralmente opuestos de una circunferencia (
) diametralmente opuestos de una circunferencia ( ), los dos segmentos que unen a estos dos puntos con un tercero de la circunferencia forman
), los dos segmentos que unen a estos dos puntos con un tercero de la circunferencia forman 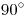 . Ahora bien, ¿cómo sabemos qué tercer punto de la circunferencia
. Ahora bien, ¿cómo sabemos qué tercer punto de la circunferencia  tomar, de manera de obtener las tangentes a
tomar, de manera de obtener las tangentes a  ? Pues bien, los segmentos
? Pues bien, los segmentos  y
y  son radios de
son radios de  , y simultáneamente
, y simultáneamente 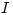 y
y  pertenecen a
pertenecen a  : por tanto, los segmentos
: por tanto, los segmentos  y
y  resultan normales respectivamente a
resultan normales respectivamente a  y a
y a  , siendo por ello tangentes a la circunferencia
, siendo por ello tangentes a la circunferencia  dada.
dada. - Tangentes exteriores: tenemos el punto
 , centro de una circunferencia
, centro de una circunferencia  de radio
de radio 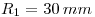 ; y a una distancia
; y a una distancia 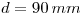 de él, el punto
de él, el punto 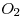 , centro de otra circunferencia
, centro de otra circunferencia 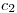 , de radio
, de radio  . Ahora imaginemos lo siguiente: que el radio
. Ahora imaginemos lo siguiente: que el radio  y el radio
y el radio 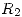 comienzan a decrecer a igual velocidad, hasta que uno de ellos (en este caso,
comienzan a decrecer a igual velocidad, hasta que uno de ellos (en este caso, 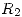 ) se hace cero. El otro (
) se hace cero. El otro ( ) resulta la diferencia entre ambos radios. ¿En qué se han convertido esas dos tangentes exteriores que buscábamos? Bueno, si uno lo mira fijo, puede notar una cierta similitud entre éste ejercicio y el anterior:
) resulta la diferencia entre ambos radios. ¿En qué se han convertido esas dos tangentes exteriores que buscábamos? Bueno, si uno lo mira fijo, puede notar una cierta similitud entre éste ejercicio y el anterior: 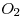 se ha convertido en análogo del
se ha convertido en análogo del  , y el
, y el  (valga la redundancia) en análogo del
(valga la redundancia) en análogo del  . ¿Qué podemos concluir, entonces? Que las tangentes que buscamos son paralelas a estas otras dos tangentes. Más aún, conocemos el método para encontrar estas otras dos tangentes que han resultado del decrecimiento de los radios. Encontrémolas, pues. Volviendo al dibujo, tracemos, con centro en
. ¿Qué podemos concluir, entonces? Que las tangentes que buscamos son paralelas a estas otras dos tangentes. Más aún, conocemos el método para encontrar estas otras dos tangentes que han resultado del decrecimiento de los radios. Encontrémolas, pues. Volviendo al dibujo, tracemos, con centro en  una circunferencia
una circunferencia  de radio igual
de radio igual 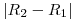 (que viene siendo igual a
(que viene siendo igual a 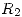 ). Luego, trazamos otra circunferencia
). Luego, trazamos otra circunferencia  , con centro en el punto medio de
, con centro en el punto medio de 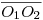 y radio
y radio  . La intersección de estas dos circunferencias nos define dos puntos de tangencia de
. La intersección de estas dos circunferencias nos define dos puntos de tangencia de  (llamémoslos
(llamémoslos 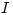 y
y  , como a los del ejercicio anterior) 1). Si ahora prolongamos el segmento
, como a los del ejercicio anterior) 1). Si ahora prolongamos el segmento  y el
y el  hasta
hasta  tenemos los puntos de tangencia de la misma. Ahora, trazando dos segmentos, respectivamente paralelos a
tenemos los puntos de tangencia de la misma. Ahora, trazando dos segmentos, respectivamente paralelos a  y a
y a  , por
, por  tenemos los otros dos puntos de tangencia que necesitábamos, sobre la segunda circunferencia (
tenemos los otros dos puntos de tangencia que necesitábamos, sobre la segunda circunferencia (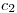 ). Podemos ahora, finalmente, trazar las tangentes exteriores que buscábamos.
). Podemos ahora, finalmente, trazar las tangentes exteriores que buscábamos. - Tangentes interiores: tenemos el punto
 , centro de una circunferencia
, centro de una circunferencia  de radio
de radio  ; y a una distancia
; y a una distancia 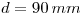 de él, el punto
de él, el punto 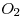 , centro de otra circunferencia
, centro de otra circunferencia 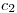 , de radio
, de radio  . El procedimiento en este caso es análogo al aplicado en los casos anteriores, aunque en éste quizá eso no sea tan explícitamente así. Para empezar, usemos nuestra imaginación nuevamente, como en la vez anterior: queremos las tangentes interiores a ambas circunferencias. Por ello, imaginemos que el radio de la primera circunferencia decrece con la misma rapidez con la que el radio de la segunda circunferencia crece , hasta que la aquélla se convierte en un punto. El problema se habría reducido (como habíamos imaginado en el caso anterior) entonces a resolver el primer ejercicio, y las tangentes que buscamos no son sino paralelas a estas dos nuevas tangentes: tangentes a una circunferencia de radio igual a
. El procedimiento en este caso es análogo al aplicado en los casos anteriores, aunque en éste quizá eso no sea tan explícitamente así. Para empezar, usemos nuestra imaginación nuevamente, como en la vez anterior: queremos las tangentes interiores a ambas circunferencias. Por ello, imaginemos que el radio de la primera circunferencia decrece con la misma rapidez con la que el radio de la segunda circunferencia crece , hasta que la aquélla se convierte en un punto. El problema se habría reducido (como habíamos imaginado en el caso anterior) entonces a resolver el primer ejercicio, y las tangentes que buscamos no son sino paralelas a estas dos nuevas tangentes: tangentes a una circunferencia de radio igual a  que pasan por el punto
que pasan por el punto  . Hallémoslas: tracemos esa circunferencia
. Hallémoslas: tracemos esa circunferencia  de centro
de centro 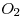 y radio
y radio  , y otra
, y otra  , con centro en el punto medio de
, con centro en el punto medio de 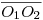 y radio también igual a
y radio también igual a  . Los puntos de intersección entre ambas (llamémoslos, en un rapto de inspiración,
. Los puntos de intersección entre ambas (llamémoslos, en un rapto de inspiración, 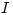 y
y  ) 2) serán (junto con
) 2) serán (junto con  ) los puntos de paso de dos tangentes a la circunferencia
) los puntos de paso de dos tangentes a la circunferencia  . Paralelas respectivamente a esas dos tangentes serán las que buscábamos en un principio. Donde los segmentos
. Paralelas respectivamente a esas dos tangentes serán las que buscábamos en un principio. Donde los segmentos 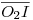 y
y  cortan a la circunferencia
cortan a la circunferencia 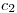 tenemos los puntos de tangencia a la misma. Para
tenemos los puntos de tangencia a la misma. Para  : trazamos una paralela a
: trazamos una paralela a  por
por  , pero del otro lado del segmento
, pero del otro lado del segmento 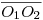 (mirando la lámina terminada se entiende mejor esta última frase). Del mismo modo se traslada una paralela a
(mirando la lámina terminada se entiende mejor esta última frase). Del mismo modo se traslada una paralela a  . Las intersecciones de estos dos últimos segmentos con
. Las intersecciones de estos dos últimos segmentos con  determinan los dos puntos de tangencia que nos restaban.
determinan los dos puntos de tangencia que nos restaban. - Tres curvas: tenemos el punto
 , centro de una circunferencia
, centro de una circunferencia  de radio
de radio 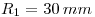 ; y a una distancia
; y a una distancia 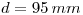 de él, el punto
de él, el punto 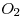 , centro de otra circunferencia
, centro de otra circunferencia 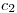 , de radio
, de radio 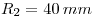 . El objetivo ahora es hallar el centro de una circunferencia
. El objetivo ahora es hallar el centro de una circunferencia 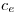 que sea simultáneamente tangente a
que sea simultáneamente tangente a  y a
y a 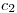 . Sabemos, por lo pronto, que el radio de dicha circunferencia
. Sabemos, por lo pronto, que el radio de dicha circunferencia 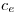 es
es  . Este problema, no lo es tanto quizás, es más bien un ejercicio pues su resolución, como se verá, es harto sencilla. Tracemos, con centro en
. Este problema, no lo es tanto quizás, es más bien un ejercicio pues su resolución, como se verá, es harto sencilla. Tracemos, con centro en  , una nueva circunferencia
, una nueva circunferencia 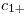 de radio
de radio  ; y con centro en
; y con centro en 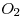 , otra nueva circunferencia
, otra nueva circunferencia  de radio
de radio  . Los dos puntos que pertenecen a
. Los dos puntos que pertenecen a  son las dos posibles soluciones a este ejercicio.
son las dos posibles soluciones a este ejercicio. - Curva y rectas: este último ejercicio no presenta mayores dificultades en cuanto a su resolución. Se tienen dos rectas, inclinadas
 una respecto de la otra, y se las quiere empalmar mediante un arco de circunferencia de radio
una respecto de la otra, y se las quiere empalmar mediante un arco de circunferencia de radio  . Para ello, a cada una de las dos rectas se le traza una paralela a una distancia igual al radio
. Para ello, a cada una de las dos rectas se le traza una paralela a una distancia igual al radio 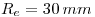 dado. La intersección de estas dos paralelas da el punto
dado. La intersección de estas dos paralelas da el punto  buscado, centro de la circunferencia
buscado, centro de la circunferencia 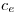 cuyo arco buscamos. Lo que nos falta, encontrar los puntos de tangencia de
cuyo arco buscamos. Lo que nos falta, encontrar los puntos de tangencia de 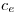 para así delimitar el arco, no es difícil: por
para así delimitar el arco, no es difícil: por  tracemos una normal a cada paralela. Donde las normales cortan a las rectas originales correspondientes, se tienen los dos puntos de tangencia buscados, y se pueden empalmar con suma belleza y gracia las susodichas rectas.
tracemos una normal a cada paralela. Donde las normales cortan a las rectas originales correspondientes, se tienen los dos puntos de tangencia buscados, y se pueden empalmar con suma belleza y gracia las susodichas rectas.

