70.03 Medios de Representación "A" - Trabajo Práctico - Desarrollo

Período: 1er Cuatrimestre 2007

Alumno: García Mendive, Iñaki

1. Desarrollo del cilindro 3: el ancho del mismo será igual a 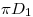, que es la longitud de la circunferencia (que es el extremo superior del cilindro). Trazamos entonces una línea de dicha longitud (que llamaremos línea de referencia), a la cual dividiremos en doce partes iguales, y desde la cual mediremos las longitudes de las generatrices que utilizamos para el desarrollo. La generatriz según la cual cortamos al cilindro (la que contiene al punto 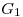) es la que se encuentra a ambos extremos de la línea trazada, y su longitud se obtiene en verdadera magnitud tanto en ortografía como en tercera proyección: se mide desde 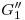(o desde 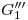) hasta el extremo superior del cilindro. Dicha longitud es luego medida sobre una perpendicular a la línea de referencia y a partir de ésta, obteniéndose 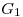en el extremo de esa perpendicular (esto se hace en ambos extremos de la línea de referencia). Para cualquier otro punto, por ejemplo el 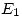, se mide en ortografía¹⁾ la longitud de la generatriz que pasa por 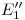, y se la lleva, a partir de la línea de referencia, sobre la perpendicular a ésta que es la cuarta línea de división.
2. Desarrollo conjunto de los cilindros 2 y 3: Al leer el procedimiento explicado en este inciso, pido al lector paciencia: primero se explicará el método a seguir y recién al final se explicitarán las razones que lo justifican. Por otra parte, para evitar confusiones es recomendable que durante toda la explicación que sigue se vea la lámina resuelta. Para empezar, trazamos el desarrollo de la circunferencia (que es límite superior del cilindro 3): un segmento de longitud igual a 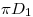. Por su extremo izquierdo le trazamos una perpendicular cuyo largo es el de la generatriz del cilindro 3 que pasa por 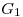(llamémosla 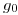)²⁾: es que esta perpendicular es en verdad el desarrollo de dicha generatriz, y es por ello que a su extremo inferior lo notamos 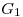. Ahora, a partir de él, prolongamos la perpendicular una distancia igual a la longitud del segmento 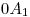³⁾. Al principio del segmento recién adosado lo rotulamos 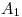, y al final lo llamamos : hemos obtenido así el desarrollo del segmento 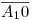⁴⁾ de la generatriz 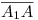del cilindro 2. Seguidamente, en el otro extremo de trazamos también el desarrollo de 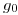y — a continuación de éste — el desarrollo del segmento 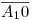de la generatriz 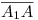. Unimos los extremos de ambos pares de desarrollos mediante un segmento 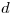idéntico a y dividimos al rectángulo resultante en doce franjas verticales, numerando a las primeras siete líneas divisorias de a , tal como se aprecia en la lámina. Vemos que la línea contiene al desarrollo de una generatriz (g_0) del cilindro 3 y, a continuación de éste, al desarrollo de un segmento (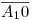) de la generatriz del cilindro 2 opuesta a 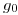la (la 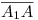). Así también, la línea conendrá al desarrollo de la generatriz 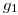(la que pasa por 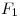) del cilindro 3 y, a continuación, al segmento que va de 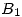hasta 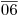de la generatriz del cilindro 2. Y así con las demás, hasta llegar a la última línea (la 12) donde está el desarrollo (que ya trazamos) idéntico al de la primera línea. Como se intuye, y como se observa en la lámina terminada, la línea es eje de simetría del rectángulo. Por todo lo dicho anteriormente, se tienen dos alternativas para trazar los desarrollos de las generatrices que restan: se mide sobre cada línea, a partir de la longitud de la generatriz pertinente del cilindro 3 (y lo que resta será el desarrollo de un segmento de la correspondiente generatriz del cilindro 2), o bien se mide sobre cada línea, a partir de 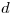, la longitud del segmento de generatriz pertinente del cilindro 2 (y lo que resta será el desarrollo de la correspondiente generatriz del cilindro 3). Cualquiera sea el camino elegido el resultado debe ser el mismo, naturalmente. Al final de este proceso se tendrá: en la parte superior del rectángulo el desarrollo del cilindro 3, y en la parte inferior del rectángulo el desarrollo de una parte del cilindro 2 (la que va desde su intersección con el 3 hasta el segmento 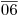(segmento que coincide con la ortografía de la circunferencia según la cual el cilindro es seccionado por un plano proyectante sobre 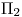). 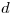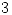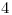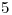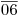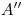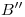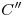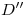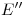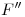Luego, para dibujar el resto del desarrollo del cilindro 2, debemos medir a partir de y sobre cada línea , , , , , y las distancias desde el segmento hasta , , , , , y 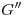, que luego se repiten en orden inverso (o sea, de 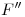a 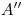) para el resto de las líneas (de la a la 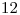), por una cuestión de simetría.
   Es así que en la porción superior de esta forma que hemos dibujado, la limitada por y la curva 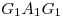, tenemos el desarrollo del cilindro 3; y en la porción restante, la que está entre las curvas 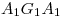y 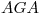, tenemos el desarrollo del cilindro 3. El hecho de que podamos trazar los desarrollos de ambos cilindros uno a continuación del otro, y más precisamente, que la transformada de la curva intersección sea la misma para ambos, responde a que la intersección entre ambos cilindros es por penetración por bitangencia, como se ha dicho ya en el segundo inciso de la lámina precedente.
3. Desarrollo del cilindro 1: Para el desarrollo de este cilindro empezaremos trazando una línea que es el desarrollo de un meridiano ⁵⁾ del mismo, similarmente al comienzo del inciso anterior. Luego, sobre una perpendicular a trazada por su punto medio, y a una distancia arbitraria de , ubicamos el segmento 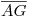cuya longitud no ha cambiado durante el desarrollo⁶⁾ y se aprecia en verdadera magnitud tanto en icnografía como en ortografía⁷⁾. Hecho esto, se marcan sobre 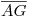los puntos 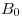, , 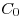, 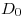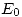y 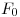, producto de trazar respectivamente por 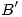, , 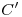, 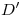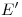y 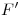normales a 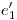. Luego, es cuestión de obtener las distancias 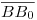etcétera, para ubicar el punto y los demás. Como se aprecia en la lámina, por ejemplo la distancia 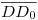se obtiene de una relación de proporcionalidad (ver lámina 9A): la longitud 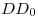es al ángul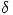o como 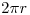es a 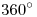. De la misma forma se pueden obtener las demás longitudes, lográndose con ello trazar el desarrollo de la intersección, que no es sino un óvalo, ligeramente más ancho que lo que se observa en icnografía, pero igual en largo.