Tabla de Contenidos
70.03 Medios de Representación "A" - Trabajo Práctico - Intersección de Cuerpos
Período: 1er Cuatrimestre 2007
Alumno: García Mendive, Iñaki
Lámina
Resolución
- Hallar la intersección entre el cilindro 2 y el cilindro 3: En ortografía tenemos los puntos
 y
y 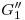 que son intersecciones entre el contorno aparente de un cilindro y el del otro. ¿Cómo sabemos que esas son intersecciones reales? Pues bien, basta observar que: los dos cilindros tienen el mismo diámetro, y sus ejes se cortan. Esto último también nos permite afirmar que esta intersección buscada, en ortografía, es el segmento
que son intersecciones entre el contorno aparente de un cilindro y el del otro. ¿Cómo sabemos que esas son intersecciones reales? Pues bien, basta observar que: los dos cilindros tienen el mismo diámetro, y sus ejes se cortan. Esto último también nos permite afirmar que esta intersección buscada, en ortografía, es el segmento 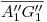 , pues se observa que es el segmento bisector de dos ángulos (los obtusos) de los cuatro que resultan de
, pues se observa que es el segmento bisector de dos ángulos (los obtusos) de los cuatro que resultan de 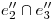 1).
1).
Nótese, sin embargo, que la intersección entre dos cilindros no puede ser un segmento de recta: no es sino una elipse degenerada. Esto se pone de manifiesto en la tercera proyección, en donde el diámetro mayor está dado por el diámetro del propio cilindro, y el menor lo determinan
no es sino una elipse degenerada. Esto se pone de manifiesto en la tercera proyección, en donde el diámetro mayor está dado por el diámetro del propio cilindro, y el menor lo determinan  y
y 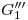 . Por ser esta elipse muy excéntrica, su trazado se puede hacer sin mayor error utilizando el método de la tarjeta. En cuanto a la visiblidad de la misma, observamos que la mitad inferior (que contiene a
. Por ser esta elipse muy excéntrica, su trazado se puede hacer sin mayor error utilizando el método de la tarjeta. En cuanto a la visiblidad de la misma, observamos que la mitad inferior (que contiene a 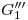 ) es invisible pues está a la derecha del cilindro 2, mientras que el resto es visible.
) es invisible pues está a la derecha del cilindro 2, mientras que el resto es visible.
En icnografía la intersección coincide, por supuesto, con el contorno aparente del cilindro 3. - Hallar la intersección entre el cilindro 1 y el cilindro 2: A este fin emplearemos planos auxiliares, paralelos al definido por
 , y que seccionarán a cada cilindro según generatrices. En la tercera proyección (donde esta intersección buscada coincide con el contorno aparente del primer cilindro) y también en icnografía están claros los planos límite: son aquellos dos cuyas trazas coinciden con el contorno aparente del segundo cilindro. Con el objetivo de ordenar nuestro método haremos uso de una circunferencia (un paralelo del cilindro) y de su abatimiento para ubicar a los siete planos auxiliares que usaremos y para ubicar a las generatrices de corte. Es así que en ortografía hemos dibujado el abatimiento de una mitad de dicha circunferencia (la otra mitad es innecesaria), a la cual hemos fraccionado en seis arcos iguales, numerándolos desde el cero. En tercera proyección observamos el abatimiento de otra semicircunferencia, dividida de igual manera, y numerada correspondientemente con la anterior. El primer plano que usaremos cortará al cilindro 2 según la generatiz que pasa por
, y que seccionarán a cada cilindro según generatrices. En la tercera proyección (donde esta intersección buscada coincide con el contorno aparente del primer cilindro) y también en icnografía están claros los planos límite: son aquellos dos cuyas trazas coinciden con el contorno aparente del segundo cilindro. Con el objetivo de ordenar nuestro método haremos uso de una circunferencia (un paralelo del cilindro) y de su abatimiento para ubicar a los siete planos auxiliares que usaremos y para ubicar a las generatrices de corte. Es así que en ortografía hemos dibujado el abatimiento de una mitad de dicha circunferencia (la otra mitad es innecesaria), a la cual hemos fraccionado en seis arcos iguales, numerándolos desde el cero. En tercera proyección observamos el abatimiento de otra semicircunferencia, dividida de igual manera, y numerada correspondientemente con la anterior. El primer plano que usaremos cortará al cilindro 2 según la generatiz que pasa por  , la cual es a su vez contorno aparente ortográfico del mismo y en tercera proyección es coincidente con
, la cual es a su vez contorno aparente ortográfico del mismo y en tercera proyección es coincidente con 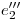 . El segundo plano cortará al segundo cilindro según la generatriz pasante por
. El segundo plano cortará al segundo cilindro según la generatriz pasante por  y según la generatriz pasante por
y según la generatriz pasante por 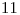 (las dos son coincidentes en ortografía 2). En tercera proyección el
(las dos son coincidentes en ortografía 2). En tercera proyección el 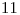 está sin denominar: es el siguiente a la izquierda del
está sin denominar: es el siguiente a la izquierda del  ). En cuanto al cilindro 1, no hemos dibujado las generatrices según las cuales es seccionado por los planos auxiliares: cada una de ellas degenera en un punto en la tercera proyección, siendo por tanto de fácil determinación con la ayuda de la ya trazada semicircunferencia abatida. Así, notamos que el plano pasante por
). En cuanto al cilindro 1, no hemos dibujado las generatrices según las cuales es seccionado por los planos auxiliares: cada una de ellas degenera en un punto en la tercera proyección, siendo por tanto de fácil determinación con la ayuda de la ya trazada semicircunferencia abatida. Así, notamos que el plano pasante por  corta al contorno aparente del cilindro 1 según una generatriz
corta al contorno aparente del cilindro 1 según una generatriz 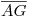 que es coincidente con
que es coincidente con  ; el plano pasante por
; el plano pasante por  lo hace según otra, coincidente con
lo hace según otra, coincidente con 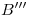 y así hasta el plano límite, que lo hace según otra coincidente con
y así hasta el plano límite, que lo hace según otra coincidente con 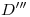 . La ortografía de cada una de estas generatrices pasa por
. La ortografía de cada una de estas generatrices pasa por  o por
o por 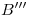 o el punto de que se trate, y es paralela al contorno aparente ortográfico del cilindro 1.
o el punto de que se trate, y es paralela al contorno aparente ortográfico del cilindro 1.
Basta de cháchara. Dispongámonos, de una vez, a hallar esta intersección. En ortografía vemos que con facilidad obtenemos ya dos puntos: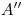 y
y 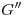 , donde se cortan los contornos aparentes de cada cilindro. En cuanto al hallazgo de otros puntos, vemos que es fácil trazar las generatrices de corte: basta dibujar (para el segundo cilindro) paralelas a
, donde se cortan los contornos aparentes de cada cilindro. En cuanto al hallazgo de otros puntos, vemos que es fácil trazar las generatrices de corte: basta dibujar (para el segundo cilindro) paralelas a 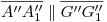 por
por  y luego cortarlas con las generatrices correspondientes del segundo cilindro (las pasantes respectivamente por
y luego cortarlas con las generatrices correspondientes del segundo cilindro (las pasantes respectivamente por 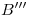 ,
, 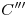 ,
, 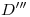 ,
, 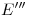 3),
3), 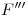 4)). La curva que obtendremos, al unir los puntos
4)). La curva que obtendremos, al unir los puntos 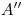 ,
, 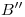 ,
, 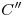 ,
, 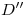 ,
, 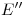 ,
, 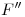 y
y 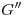 será una rama de hipérbola, cuyas asíntotas son las dos rectas bisectrices de los cuatro ángulos que resultan de intersecar
será una rama de hipérbola, cuyas asíntotas son las dos rectas bisectrices de los cuatro ángulos que resultan de intersecar  con
con  . La segunda rama de la hipérbola está del lado opuesto del vértice (
. La segunda rama de la hipérbola está del lado opuesto del vértice (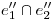 ) de la misma, y es la curva según la cual el cilindro 2 (si lo continuáramos hacia abajo) volvería a penetrar al cilindro 1. El hecho de que esta intersección sea en ortografía una hipérbola se debe a que los ejes se cortan y los diámetros son distintos. Ahora imaginemos que el diámetro del cilindro 2 aumenta progresivamente hasta hacerse igual al del cilindro 1: la intersección sería por penetración por bitangencia y obtendríamos como ortografía de ella las dos asíntotas de la hipérbola. Y esto, querido lector, es precisamente lo que sucede en el inciso precedente:
) de la misma, y es la curva según la cual el cilindro 2 (si lo continuáramos hacia abajo) volvería a penetrar al cilindro 1. El hecho de que esta intersección sea en ortografía una hipérbola se debe a que los ejes se cortan y los diámetros son distintos. Ahora imaginemos que el diámetro del cilindro 2 aumenta progresivamente hasta hacerse igual al del cilindro 1: la intersección sería por penetración por bitangencia y obtendríamos como ortografía de ella las dos asíntotas de la hipérbola. Y esto, querido lector, es precisamente lo que sucede en el inciso precedente: 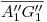 es una asíntota, y la otra es la recta bisectriz de los dos ángulos agudos que resultan de
es una asíntota, y la otra es la recta bisectriz de los dos ángulos agudos que resultan de 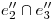 . Si el diámetro de alguno de los dos cilindros (el 2 ó el 3) cambiara, se tendría allí el mismo caso que encontramos en este segundo inciso, denominado penetración total.
. Si el diámetro de alguno de los dos cilindros (el 2 ó el 3) cambiara, se tendría allí el mismo caso que encontramos en este segundo inciso, denominado penetración total.
La curva de intersección en icnografía se obtiene, por ejemplo para el punto , de la siguiente manera: se baja por
, de la siguiente manera: se baja por 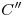 una vertical. Ahora, se prolonga el contorno aparente icnográfico del cilindro 1 hacia la derecha, y se traza una tangente al contorno aparente en tercera proyección del cilindro 1 hacia abajo: donde se corten, tendremos un punto que servirá como centro de giro para trasladar puntos desde la tercera proyección hasta la icnografía. Bajamos entonces, ahora, una vertical por
una vertical. Ahora, se prolonga el contorno aparente icnográfico del cilindro 1 hacia la derecha, y se traza una tangente al contorno aparente en tercera proyección del cilindro 1 hacia abajo: donde se corten, tendremos un punto que servirá como centro de giro para trasladar puntos desde la tercera proyección hasta la icnografía. Bajamos entonces, ahora, una vertical por 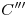 hasta que corte a la prolongación del contorno aparente icnográfico del cilindro 1. Giramos en sentido horario hasta cortar a la tangente al contorno aparente en tercera proyección del cilindro 1, y de allí trazamos una horizontal hasta cortar a la vertical bajada desde
hasta que corte a la prolongación del contorno aparente icnográfico del cilindro 1. Giramos en sentido horario hasta cortar a la tangente al contorno aparente en tercera proyección del cilindro 1, y de allí trazamos una horizontal hasta cortar a la vertical bajada desde 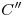 . Tenemos entonces a
. Tenemos entonces a 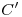 . Nótese que la curva que así se encontrará será en realidad una mitad de la curva intersección. Para encontrar la otra mitad basta saber que la curva intersección es simétrica respecto de
. Nótese que la curva que así se encontrará será en realidad una mitad de la curva intersección. Para encontrar la otra mitad basta saber que la curva intersección es simétrica respecto de  . Para encontrar, ejempligracia, el simétrico de
. Para encontrar, ejempligracia, el simétrico de 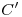 , se puede llevar la distancia de
, se puede llevar la distancia de 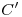 a
a  al otro lado del eje (sobre una vertical trazada por
al otro lado del eje (sobre una vertical trazada por 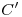 ). Esta curva intersección es un ovoide u óvalo y en cuanto a su visibilidad, notamos que el arco que parte de
). Esta curva intersección es un ovoide u óvalo y en cuanto a su visibilidad, notamos que el arco que parte de 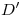 , pasa por
, pasa por 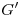 y termina en el simétrico de
y termina en el simétrico de 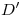 es invisible, pues está debajo del cilindro 2, mientras que el resto es visible.
es invisible, pues está debajo del cilindro 2, mientras que el resto es visible.
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
1)
Se ampliará más adelante a este respecto, al tratarse la intersección entre los cilindros 1 y 2
2)
De ahí que no se haya dibujado el rebatimiento de la circunferencia entera ni sus doce divisiones.
3)
Coincidente con 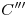 , aunque no se lo nombre en la tercera proyección.
, aunque no se lo nombre en la tercera proyección.
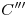 , aunque no se lo nombre en la tercera proyección.
, aunque no se lo nombre en la tercera proyección.4)
Coincidente con 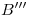 , aunque no se lo nombre en la tercera proyección.
, aunque no se lo nombre en la tercera proyección.
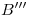 , aunque no se lo nombre en la tercera proyección.
, aunque no se lo nombre en la tercera proyección.Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported



