70.03 Medios de Representación "A" - Trabajo Práctico - Helicoide y Desarrollo

Período: 1er Cuatrimestre 2007

Alumno: García Mendive, Iñaki

1. Hallar la transformada de la hélice: Como el radio de curvatura 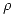de la hélice es constante para todo punto de la misma, el radio de curvatura 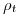de su transformada será también constante. Esta transformada será entonces un arco de circunferencia, y 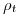será (por el Teorema de Catalán) casualmente igual a 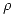. En cuanto a la amplitud de dicho arco, ésta viene dada por la fórmula 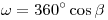, cuya deducción está apuntada en la lámina resuelta (extraída a su vez del Tomo II del Ingeniero Di Lorenzo, parágrafo 52 (página 94)).
2. Hallar el desarrollo del helicoide: Para esto, subdividiremos a la transformada en ocho arcos iguales, y le trazaremos las tangentes por cada marca de división: las longitudes de cada una es la longitud de arco comprendida entre el punto considerado y el punto inicial () del arco, pues el 'borde exterior' del desarrollo del helicoide es la involuta de la transformada. Las longitudes de las tangentes 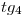y 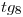las tenemos en verdadera magnitud en elevación en la lámina 11A. En cuanto al resto, podemos trabajar sobre dicha lámina (mediante giros, abatimientos o cambios de planos) para encontrar su verdadera magnitud. Sin embargo, para no recargar de líneas a la lámina (y, además, para no acumular errores), encontraremos las longitudes que necesitamos mediante fórmulas analíticas. Así, por ejemplo, para la tangente 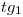en , su longitud 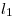viene dada por la relación de proporcionalidad: 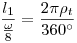, donde es el ángulo que limita al arco 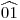. Y así podemos encontrar la longitud de cualquiera de las otras tangentes, cuidando de cambiar por el valor que corresponda en cada caso. Unidos los extemos de las ocho tangentes tenemos la involuta de la transformada, que es el borde del desarrollo del helicoide. Para poder construir el helicoide a partir de la lámina se lo debe recortar por 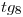, continuando por el borde del desarrollo, y finalizando por la transformada. Es decir que el fragmento de círculo limitado por y la transformada debe ser desechado.