Tabla de Contenidos
70.03 Medios de Representación "A" - Trabajo Práctico - Hélice & Helicoide
Período: 1er Cuatrimestre 2007
Alumno: García Mendive, Iñaki
Lámina
Resolución
- Hallar las proyecciones icnográfica y ortográfica de la hélice: A este fin debemos primero trazar los correspondientes contornos aparentes del cilindro que la contiene. En icnografía, a
 de la fundamental y a
de la fundamental y a  del margen derecho de la lámina, ubicamos el centro de una circunferencia
del margen derecho de la lámina, ubicamos el centro de una circunferencia  de radio
de radio  . Circunferencia que será simultáneamente contorno aparente icnográfico del cilindro y de la hélice. En ortografía dibujamos un réctángulo de alto
. Circunferencia que será simultáneamente contorno aparente icnográfico del cilindro y de la hélice. En ortografía dibujamos un réctángulo de alto  y de ancho igual a
y de ancho igual a  .
.
Para hallar la ortografía de la hélice: dividimos a la circunferencia en icnografía en un cierto número de partes iguales (ocho, en este caso), y al paso (la altura del cilindro) en ortografía en el mismo número de partes iguales. Las icnografías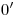 ,
, 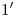 ,
, 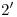 , …
, … 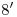 de los puntos de la hélice se encuentran sobre
de los puntos de la hélice se encuentran sobre  en las marcas de división efectuadas. El punto en ortografía (
en las marcas de división efectuadas. El punto en ortografía ( ,
, 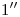 ,
, 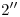 , …
, … 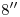 ) que le corresponde a cada uno de ellos se encuentra levantando por
) que le corresponde a cada uno de ellos se encuentra levantando por 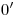 ,
, 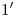 ,
, 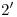 , …
, … 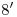 una vertical hasta cortar respectivamente a la fundamental, a la primera línea con la que se dividió al cilindro, a la segunda línea, … a la octava línea (que es la última, y es por ello también parte del contorno aparente ortográfico del cilindro). La unión de los puntos
una vertical hasta cortar respectivamente a la fundamental, a la primera línea con la que se dividió al cilindro, a la segunda línea, … a la octava línea (que es la última, y es por ello también parte del contorno aparente ortográfico del cilindro). La unión de los puntos  ,
, 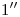 ,
, 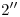 , …
, … 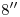 así obtenidos resulta en una sinusoide. Nótese que, por quedar detrás del cilindro, la fracción de curva comprendida entre
así obtenidos resulta en una sinusoide. Nótese que, por quedar detrás del cilindro, la fracción de curva comprendida entre 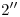 y
y 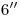 es invisible, mientras que el resto es visible.
es invisible, mientras que el resto es visible. - Hallar las proyecciones en planta y en elevación del helicoide: El helicoide desarrollable está formado por la unión de las tangentes a la hélice en cada uno de sus puntos. Nosotros, naturalmente, no trazaremos todas esas tangentes, sino que nos avocaremos a dibujar las que corresponden a los puntos
 ,
,  ,
,  , …
, … 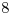 cuyas proyecciones acabamos de obtener.
cuyas proyecciones acabamos de obtener.
Primero trabajaremos en planta: para esto es convieniente saber que la traza del helicoide sobre el icnográfico es la involuta o desarrollante de la circunferencia ,1) lo que implica que la longitud de la icnografía de cada tangente
,1) lo que implica que la longitud de la icnografía de cada tangente 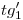 ,
,  , …
, … 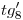 será igual al arco de
será igual al arco de  comprendido entre
comprendido entre 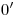 y el punto
y el punto 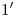 ,
, 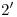 …
… 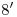 en cuestión. Así, por ejemplo, la longitud de
en cuestión. Así, por ejemplo, la longitud de  es igual al arco de
es igual al arco de  comprendido entre
comprendido entre 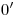 y
y 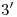 . Uniendo los extremos de cada una de las tangentes, tenemos la curva, traza icnográfica del helicoide desarrollable.
. Uniendo los extremos de cada una de las tangentes, tenemos la curva, traza icnográfica del helicoide desarrollable.
Y para encontrar la ortografía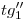 ,
, 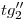 …
… 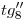 de cada tangente se levanta por el extremo de cada
de cada tangente se levanta por el extremo de cada 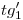 ,
,  …
… 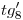 (es decir, por cada
(es decir, por cada 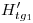 ,
, 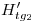 …
… 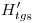 ) una vertical hasta cortar a la fundamental en
) una vertical hasta cortar a la fundamental en 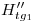 ,
, 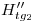 …
… 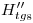 , respectivamente. Uniendo
, respectivamente. Uniendo 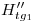 ,
, 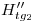 …
… 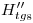 con el correspondiente punto
con el correspondiente punto 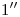 ,
, 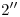 …
… 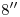 se obtiene la ortografía buscada para cada tangente. Así, por ejemplo para
se obtiene la ortografía buscada para cada tangente. Así, por ejemplo para 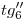 se levanta por el extremo de
se levanta por el extremo de  (por la traza icnográfica
(por la traza icnográfica 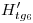 ) una vertical (que coincide con
) una vertical (que coincide con  ) hasta cortar a la fundamental en
) hasta cortar a la fundamental en 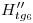 , punto que unimos con
, punto que unimos con 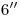 para obtener
para obtener 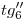 (que es coincidente con el lateral izquierdo del contorno aparente ortográfico del cilindro). Nótese que el ángulo
(que es coincidente con el lateral izquierdo del contorno aparente ortográfico del cilindro). Nótese que el ángulo 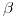 (ángulo que forman tangentes a la hélice con el plano de la base del cilindro (que en este caso es
(ángulo que forman tangentes a la hélice con el plano de la base del cilindro (que en este caso es 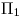 )) se aprecia en verdadera magnitud tanto en
)) se aprecia en verdadera magnitud tanto en 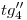 como en
como en 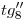 . Verifíquese también que
. Verifíquese también que 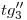 sea paralela a
sea paralela a 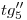 .
.
En lo que a visiblidad concierne, en icnografía todo el helicoide es visible. En ortografía, en cambio, las porciones del mismo que se encuentran detrás del cilindro (a saber, ciertos segmentos de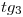 ,
, 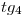 y
y 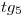 ) son invisibles y se dibujan por ello en línea de trazos. Es importante remarcar lo siguiente: hay ciertas partes del cilindro que en ortografía son invisibles pues están precedidas por el helicoide. La primera, que no es muy difícil de notar, está tapada por la parte del helicoide limitada por la tangente en
) son invisibles y se dibujan por ello en línea de trazos. Es importante remarcar lo siguiente: hay ciertas partes del cilindro que en ortografía son invisibles pues están precedidas por el helicoide. La primera, que no es muy difícil de notar, está tapada por la parte del helicoide limitada por la tangente en  y la tangente en
y la tangente en  . A pesar de esto, la porción de contorno aparente ortográfico del cilindro afectada no se dibuja en línea de trazos pues coincide con
. A pesar de esto, la porción de contorno aparente ortográfico del cilindro afectada no se dibuja en línea de trazos pues coincide con 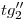 . Es así que esta primera región invisible no presenta mayor relevancia. En cuanto a la segunda parte que nos ocupa, ésta es tapada por una mínima fracción del helicoide: la limitada por la tangente en
. Es así que esta primera región invisible no presenta mayor relevancia. En cuanto a la segunda parte que nos ocupa, ésta es tapada por una mínima fracción del helicoide: la limitada por la tangente en  por y la tangente en
por y la tangente en 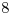 . Es así que el segmento del lateral izquierdo del contorno aparente ortográfico del cilindro que comienza en
. Es así que el segmento del lateral izquierdo del contorno aparente ortográfico del cilindro que comienza en 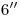 y termina en su intersección con
y termina en su intersección con 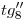 es invisible y lo dibujamos por ello en línea de trazos (en la lámina resuelta ni ha sido dibujado en línea de trazos, ha sido dejado en trazado previo).
es invisible y lo dibujamos por ello en línea de trazos (en la lámina resuelta ni ha sido dibujado en línea de trazos, ha sido dejado en trazado previo). - Hallar la evoluta de la hélice: Para esto debemos hallar el radio de curvatura
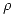 de la hélice, que es constante para cada punto de la misma. A tal fin utilizaremos un método gráfico que consiste en lo siguiente: por la esquina inferior derecha del rectángulo, que es el contorno aparente ortográfico del cilindro, trazamos una paralela
de la hélice, que es constante para cada punto de la misma. A tal fin utilizaremos un método gráfico que consiste en lo siguiente: por la esquina inferior derecha del rectángulo, que es el contorno aparente ortográfico del cilindro, trazamos una paralela 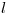 a
a 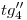 tal que el ángulo formado entre
tal que el ángulo formado entre 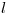 y la fundamental (
y la fundamental ( ) sea
) sea 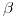 . Donde
. Donde 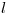 corta a la ortografía
corta a la ortografía  del eje
del eje 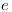 del cilindro le trazamos una perpendicular
del cilindro le trazamos una perpendicular 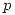 hasta cortar a la fundamental. El segmento limitado por
hasta cortar a la fundamental. El segmento limitado por 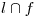 y por
y por 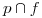 tiene la longitud
tiene la longitud 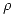 buscada. Este radio, visto así en verdadera magnitud, corresponde a los puntos
buscada. Este radio, visto así en verdadera magnitud, corresponde a los puntos  y
y  de la hélice, por lo que si llevamos un segmento de longitud
de la hélice, por lo que si llevamos un segmento de longitud 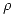 a la izquierda de
a la izquierda de 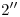 y a la derecha de
y a la derecha de 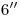 tenemos la ortografía
tenemos la ortografía 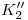 y
y  del centro de curvatura de cada uno de los dos puntos. ¿Cómo encontramos el centro de curvatura para cada punto restante? Pues bien, hallemos primero las icnografías
del centro de curvatura de cada uno de los dos puntos. ¿Cómo encontramos el centro de curvatura para cada punto restante? Pues bien, hallemos primero las icnografías  y
y 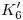 : bajamos por
: bajamos por 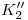 y por
y por  respectivamente una vertical hasta cortar a
respectivamente una vertical hasta cortar a  . La icnografía de la evoluta 2) será una circunferencia de radio
. La icnografía de la evoluta 2) será una circunferencia de radio  , concéntrica con la icnografía de la hélice. Subiendo por cada
, concéntrica con la icnografía de la hélice. Subiendo por cada 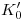 ,
,  …
…  una vertical hasta cortar respectivamente a la fundamental
una vertical hasta cortar respectivamente a la fundamental  , a la primera línea de división, … a la última línea, tenemos las ortografías
, a la primera línea de división, … a la última línea, tenemos las ortografías 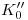 ,
, 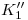 …
…  de los centros de curvatura que buscábamos. Unidas estas ortografías se obtiene una sinusoide invertida y de menor amplitud que la original. La proyección vertical de la evoluta es enteramente invisible pues se encuentra dentro del cilindro.
de los centros de curvatura que buscábamos. Unidas estas ortografías se obtiene una sinusoide invertida y de menor amplitud que la original. La proyección vertical de la evoluta es enteramente invisible pues se encuentra dentro del cilindro. - Hallar el Triedro de Frenet en el punto 3: primero hallaremos las trazas del plano
 osculador de la hélice: éste está determinado por la tangente (
osculador de la hélice: éste está determinado por la tangente (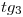 ) y por la normal principal (
) y por la normal principal (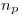 ). A la tangente ya la tenemos pues es parte del helicoide. La normal principal, de las infinitas normales a la hélice en
). A la tangente ya la tenemos pues es parte del helicoide. La normal principal, de las infinitas normales a la hélice en 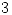 (que forman un plano normal), es aquella que contiene al centro de curvatura
(que forman un plano normal), es aquella que contiene al centro de curvatura  .
. 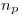 será por ello horizontal, cuyas trazas
será por ello horizontal, cuyas trazas  y
y  se encuentran fácilmente. En cuanto a su visibilidad,
se encuentran fácilmente. En cuanto a su visibilidad,  es invisible desde
es invisible desde  hasta su intersección con
hasta su intersección con 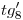 pues en ese tramo está debajo del helicoide; por otra parte, el segmento de
pues en ese tramo está debajo del helicoide; por otra parte, el segmento de  donde
donde 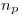 se encuentra dentro y/o detrás del cilindro también es invisible (en icnografía los puntos que limitan este segmento son
se encuentra dentro y/o detrás del cilindro también es invisible (en icnografía los puntos que limitan este segmento son  y
y 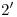 ). Ahora que tenemos las dos proyecciones de estas dos rectas, dibujemos las trazas de
). Ahora que tenemos las dos proyecciones de estas dos rectas, dibujemos las trazas de  :
:  pasa por el extremo de
pasa por el extremo de  (donde
(donde 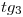 corta a
corta a 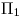 ) y es paralela a
) y es paralela a  . A
. A 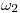 lo trazamos por donde
lo trazamos por donde  corta a la fundamental y por
corta a la fundamental y por  . Gracias a que hemos obtenido las trazas del osculador, podemos ahora trazar
. Gracias a que hemos obtenido las trazas del osculador, podemos ahora trazar 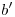 y
y 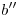 , proyecciones de la binormal que le es ortogonal. Así, por
, proyecciones de la binormal que le es ortogonal. Así, por 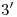 trazamos
trazamos 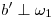 coincidente con
coincidente con  . Acto seguido, por
. Acto seguido, por 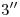 trazamos
trazamos  , con la ayuda de la cual encontramos
, con la ayuda de la cual encontramos 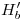 .
. 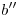 es invisible desde
es invisible desde  hasta donde corta al contorno aparente del cilindro.
hasta donde corta al contorno aparente del cilindro.
Ahora que tenemos las tres rectas que definen al triedro, sólo resta encontrar los dos planos tangente y normal. Empecemos por el tangente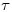 : será proyectante sobre el icnográfico pues las dos rectas
: será proyectante sobre el icnográfico pues las dos rectas 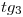 y
y  que lo determinan se proyectan coincidentemente en icnografía. Así, será
que lo determinan se proyectan coincidentemente en icnografía. Así, será  , y
, y 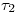 perpendicular a la fundamental, trazada por donde
perpendicular a la fundamental, trazada por donde 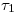 corta a la línea de tierra. En cuanto al plano normal
corta a la línea de tierra. En cuanto al plano normal 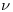 (determinado por
(determinado por 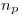 y
y  ), su traza horizontal
), su traza horizontal 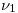 será paralela a
será paralela a  y pasará por
y pasará por 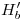 .
.  pasará por donde
pasará por donde  corta a la fundamental y por
corta a la fundamental y por  . Queda así concluido el trazado del triedro de Frenet y con esto, el de la lámina.
. Queda así concluido el trazado del triedro de Frenet y con esto, el de la lámina.
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported




