70.03 Medios de Representación "A" - Trabajo Práctico - Cicloides

Período: 1er Cuatrimestre 2007

Alumno: García Mendive, Iñaki

Artículo en Mathworld sobre la cicloide corta (en inglés)
Artículo en Mathworld sobre la cicloide normal (en inglés)
Artículo en Mathworld sobre la cicloide larga (en inglés)
Applet Java que traza hipotrocoides, trocoides y epitrocoides (en inglés)

Datos:

Radio de la ruleta.

1. Dibujar la base y las dos ruletas iniciales: si la ruleta ha de rodar sin deslizar sobre la base, dando una vuelta completa, entonces la base ha de tener una longitud de , siendo el radio de la ruleta. Una vez dibujada ésta y la base, dividimos la ruleta en ocho (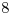) arcos iguales, y así también a la base, en ocho segmentos de longitud 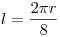. Ahora, a cada uno de los dos extremos de la base, adosamos dos segmentos de longitud 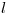.¹⁾ Hecho esto, se traza una horizontal que pase por 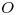, centro de la ruleta inicial, y en dicha horizontal marcamos los mismos segmentos de longitud 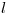que habíamos delimitado antes en la base: éstas serán las sucesivas posiciones del centro de la ruleta, a medida que ésta ruede sin deslizar sobre la base. Numeramos luego dichos segmentos, desde 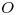hasta (como vemos, los cuatro segmentos anexados a los extremos de la base y de la horizontal no han sido nominados). A las divisiones de la ruleta también se las numera, en sentido horario y empezando por el punto posterior al de tangencia, del al ; y por cada uno de estos puntos trazamos horizontales que abarquen todo el largo de la base: , , y 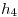. Como paso final, dibujamos la circunferencia exterior de radio 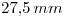²⁾, que contiene al punto que describe la cicloide larga. A esta última circunferencia también se la divide en ocho arcos iguales, y se trazan horizontales por los puntos que limitan dichos arcos, similarmente a lo recién explicado para la circunferenca menor.
2. Trazar la cicloide normal: Para ello clavamos el compás en 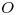y lo extendemos hasta un punto cualquiera de la ruleta. Tenemos así el radio en el compás, y la podemos transportar a cada punto sucesivo del centro de la ruleta (). Clavamos entonces el compás en sobre la horizontal trazada por 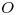, y trazamos un arco que corte a la horizontal 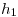: éste será un segundo punto de la cicloide normal (recordar que el primer punto es el de tangencia de la ruleta original y la base). Así se puede continuar para las demás posiciones sucesivas del centro 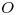de la ruleta. Cabe destacar que para el punto 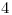el punto de la cicloide estará en la intersección de 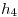con una vertical trazada por el mismo.
   En cuanto al trazado de tangentes a los puntos de la cicloide encontrados, vamos a razonar lo siguiente: que la rueda gire sin deslizar sobre la base equivale a decir que el punto de tangencia de la ruleta y la base (punto de la ruleta) tiene velocidad cero respecto de la base. Si esto es así, y si es cierto que los demás puntos de la rueda ³⁾ se trasladan mientras que no, entonces podemos afirmar que el punto en cuestión es centro instantáneo de rotación, o centro instantáneo de curvatura. Como tal, cualquier segmento que se trace desde éste a la cicloide será un radio instantáneo de curvatura, y será por tanto normal a la cicloide. La normal a este radio será la tangente a la cicloide en el punto. Esto se puede aplicar para cualquier punto de la curva, pero por conveniencia lo hacemos sólo con puntos que hemos obtenido. Caben destacar las siguientes tangentes: la tangente al punto correspondiente 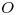al y al 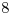son normales a la base, y la tangente en el punto correspondiente a la posición 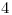es horizontal.
3. Trazar la cicloide larga: En este caso se procede de forma muy similar al anterior. Se clava el compás en las sucesivas posiciones , y se trazan arcos (con un radio igual al de la circunferencia mayor) que corten a las horizontales trazadas por los puntos de la circunferencia mayor (los puntos que delimitan los ocho arcos iguales en dicha circunferencia). El trazado de las tangentes sigue los mismos razonamientos que en el caso anterior.

En cuanto a los dos segmentos de longitud 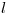adosados a cada extremo de la base: éstos sirven para trazar las continuaciones de las dos curvas hacia ambos lados. Para la cicloide normal el punto inicial (el correspondiente a 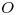) y el final (correspondiente a ) resultan puntos de retroceso de primera especie. Para la cicloide larga, se completa un bucle en cada extremo (obteniéndose, con cada bucle, un punto doble).

Recordar la utilidad de tener las tangentes en los puntos extremos de los segmentos de curva, al buscar curvas con el pistolete.