Parcialito - 70.03. Medios de Representación "A" - XX/05/2007
Cátedra: 002 — Botet - Sande - Vergez.
Fecha: 1° (y única) Oportunidad - 1° Cuatrimestre 2007
Día: XX/04/2007
Enunciado
Punto I
Datos: 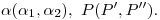
Hallar: 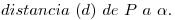
Hoja de Datos y Resolución HAY UN ERROR en la resolución1), alguien corríjalo por favor.
Punto II
Datos: 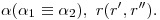
Hallar: 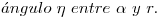
Punto III
Datos: 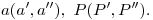
Hallar: 
Resolución
Punto I
Hoja de Datos y Resolución HAY UN ERROR en la resolución2), alguien corríjalo por favor.
Para empezar, debemos hacer lo que se llama determinar la magnitud que se quiere obtener. Esto es, en este caso, encontrar el segmento de la normal  del plano que se quiere en verdadera magnitud. Para ello es necesario, en principio, encontrar las proyecciones del punto
del plano que se quiere en verdadera magnitud. Para ello es necesario, en principio, encontrar las proyecciones del punto 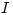 intersección de
intersección de  con
con  . Bueno, en realidad primero deberíamos trazar las proyecciones de
. Bueno, en realidad primero deberíamos trazar las proyecciones de  :
: 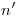 se traza perpendicular a
se traza perpendicular a 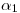 y pasante por
y pasante por 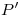 ;
; 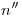 se traza perpendicular a
se traza perpendicular a 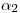 y pasante por
y pasante por 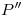 . Ahora sí, estamos en condiciones de hallar
. Ahora sí, estamos en condiciones de hallar 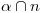 , para lo cual usaremos un cómodo y muy conveniente plano
, para lo cual usaremos un cómodo y muy conveniente plano 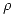 , proyectante sobre el ortográfico, y tal que su traza
, proyectante sobre el ortográfico, y tal que su traza 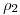 sea coincidente con
sea coincidente con 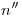 3). La recta
3). La recta 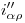 también coincide con
también coincide con 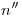 , y en la intersección de esa con
, y en la intersección de esa con 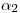 tenemos
tenemos 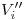 , al cual bajamos hasta la línea de tierra para encontrar
, al cual bajamos hasta la línea de tierra para encontrar 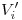 . Unimos este con la intersección de
. Unimos este con la intersección de 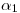 con
con 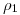 y tenemos
y tenemos  . La intersección entre esta y
. La intersección entre esta y 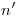 me define
me define 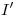 , icnografía del punto
, icnografía del punto 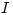 que buscamos. Su ortografía
que buscamos. Su ortografía 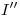 se obtiene levantando una vertical desde
se obtiene levantando una vertical desde 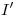 hasta
hasta 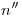 . Hemos entonces determinado la magnitud.
Ahora queremos ese segmento, el
. Hemos entonces determinado la magnitud.
Ahora queremos ese segmento, el 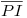 en verdadera magnitud. Para ello giraremos la recta
en verdadera magnitud. Para ello giraremos la recta  según un eje perpendicular a
según un eje perpendicular a 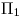 y pasante por
y pasante por  : con centro en
: con centro en 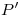 y extremo en
y extremo en 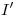 trazamos un arco de circunferencia y lo intersectamos con una horizontal pasante por
trazamos un arco de circunferencia y lo intersectamos con una horizontal pasante por 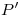 . Así encontramos
. Así encontramos 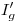 , y a
, y a 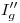 lo encontramos en la intersección de una vertical trazada por
lo encontramos en la intersección de una vertical trazada por 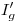 con una horizontal trazada por
con una horizontal trazada por 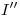 . Podemos trazar entonces tanto
. Podemos trazar entonces tanto 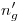 como
como 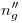 . Y es sobre esta última que podemos medir la longitud del segmento
. Y es sobre esta última que podemos medir la longitud del segmento 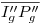 , que es la distancia
, que es la distancia 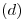 que nos pedían.
que nos pedían.
Punto II

Como se hace habitualmente en este tipo de ejercicios, lo que se busca en realidad es el ángulo entre la normal  del plano y la recta dada. Así que es esto precisamente lo que haremos. Nos ahorramos, con este método, encontrar la intersección entre el plano y la recta. Tracemos entonces la normal al plano, que es cualquiera que intersecte a
del plano y la recta dada. Así que es esto precisamente lo que haremos. Nos ahorramos, con este método, encontrar la intersección entre el plano y la recta. Tracemos entonces la normal al plano, que es cualquiera que intersecte a  .4) Trazamos entonces
.4) Trazamos entonces 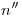 perpendicular a
perpendicular a 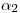 , y bajemos el punto
, y bajemos el punto 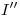 donde corte a
donde corte a 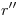 , mediante una vertical, a
, mediante una vertical, a 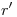 , para por allí (
, para por allí (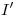 ) trazar
) trazar 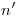 ortogonal a
ortogonal a 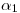 . Acabamos de determinar la magnitud. Para llevar la verdadera magnitud, que es el paso siguiente, vamos a abatir las dos rectas en cuestión sobre un plano
. Acabamos de determinar la magnitud. Para llevar la verdadera magnitud, que es el paso siguiente, vamos a abatir las dos rectas en cuestión sobre un plano 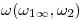 horizontal, que por comodidad (y nada más que por eso) haremos pasar por la intersección entre
horizontal, que por comodidad (y nada más que por eso) haremos pasar por la intersección entre 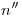 y
y 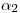 . Nuestro eje de abatimiento
. Nuestro eje de abatimiento 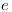 coincide en ortografía con
coincide en ortografía con 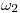 , y su icnografía se determina fácilmente, bajando el punto de intersección de
, y su icnografía se determina fácilmente, bajando el punto de intersección de  con
con 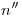 a
a 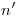 , y bajando el punto de intersección de
, y bajando el punto de intersección de  con
con 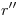 a
a 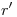 . Trazamos por
. Trazamos por 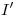 una paralela y una perpendicular a
una paralela y una perpendicular a 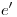 . Sobre la paralela medimos la diferencia de alturas entre
. Sobre la paralela medimos la diferencia de alturas entre  y
y 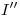 y encontramos
y encontramos  . Con el compás clavado en la intersección de la susodicha perpendicular con
. Con el compás clavado en la intersección de la susodicha perpendicular con 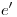 , y el extremo en
, y el extremo en  , giramos hasta cortar (más allá de
, giramos hasta cortar (más allá de 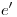 ) a la perpendicular (valga la repetición), y encontramos entonces (I). Uniéndolo con los puntos de intersección de
) a la perpendicular (valga la repetición), y encontramos entonces (I). Uniéndolo con los puntos de intersección de 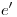 con
con 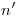 , y de
, y de 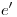 con
con 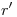 (que permanecieron inmóviles durante el abatimiento), obtenemos respectivamente
(que permanecieron inmóviles durante el abatimiento), obtenemos respectivamente 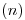 y
y 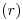 . El ángulo agudo (
. El ángulo agudo ( ) entre ellas es el buscado, y para encontrar el
) entre ellas es el buscado, y para encontrar el  que nos pedían, simplemente restamos
que nos pedían, simplemente restamos  a un ángulo recto.
a un ángulo recto.
Punto III

En este ejercicio los pasos a seguir son los siguientes: fabricarse un plano  perpendicular a
perpendicular a  y que contenga a
y que contenga a  , encontrar el punto
, encontrar el punto 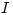 intersección de
intersección de  con
con  , unir
, unir 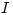 con
con  , y llevar la verdadera magnitud
, y llevar la verdadera magnitud 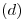 del segmento
del segmento  .
Para lo primero, vamos a trazar una horizontal
.
Para lo primero, vamos a trazar una horizontal 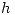 , cuya ortografía
, cuya ortografía 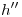 paralela a la línea de tierra pase por
paralela a la línea de tierra pase por 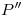 , y cuya icnografía
, y cuya icnografía  perpendicular a
perpendicular a 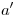 pase por
pase por 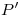 . Acto seguido, trazamos una frental
. Acto seguido, trazamos una frental  , cuya icnografía
, cuya icnografía 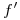 paralela a la línea de tierra pase por
paralela a la línea de tierra pase por 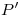 , y cuya ortografía
, y cuya ortografía 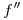 perpendicular a
perpendicular a 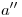 pase por
pase por 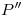 . Queda así rápidamente definido el plano
. Queda así rápidamente definido el plano  que buscábamos.
Para lo segundo, que es en realidad la parte más engorrosa de todo el ejercicio, vamos a usar un plano proyectante sobre el ortográfico
que buscábamos.
Para lo segundo, que es en realidad la parte más engorrosa de todo el ejercicio, vamos a usar un plano proyectante sobre el ortográfico 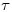 . La traza ortográfica
. La traza ortográfica 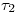 de
de 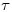 la hacemos coincidir con
la hacemos coincidir con 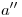 : nombramos
: nombramos 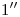 a la intersección de
a la intersección de 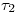 con
con 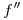 , y
, y 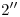 a la intersección de
a la intersección de 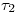 con
con 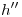 . Bajamos
. Bajamos 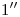 y
y 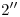 mediante verticales, a
mediante verticales, a 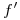 y
y  respectivamente. Uniendo
respectivamente. Uniendo 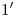 con
con 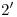 tenemos
tenemos 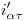 , cuya intersección con
, cuya intersección con 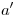 nos da la icnografía
nos da la icnografía 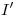 del punto
del punto 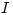 que buscábamos. Su ortografía
que buscábamos. Su ortografía 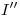 se encuentra en la intersección de una vertical trazada por
se encuentra en la intersección de una vertical trazada por 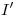 con
con 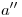 . Hemos determinado entonces la magnitud, si unimos a
. Hemos determinado entonces la magnitud, si unimos a 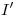 con
con 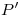 , y a
, y a 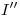 con
con 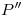 .5)
Para esta última parte giraremos la recta
.5)
Para esta última parte giraremos la recta  en torno de un eje
en torno de un eje 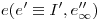 pasante por
pasante por 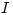 , para ello clavamos el compás en
, para ello clavamos el compás en 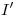 y colocando su extremo en
y colocando su extremo en 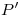 trazamos un arco que corte a una horizontal trazada por
trazamos un arco que corte a una horizontal trazada por 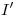 . Allí encontramos
. Allí encontramos 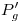 .
. 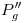 se encuentra en la intersección de una horizontal trazada por
se encuentra en la intersección de una horizontal trazada por 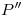 con una vertical trazada por
con una vertical trazada por 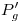 . Uniendo
. Uniendo  con
con 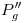 tenemos la verdadera magnitud
tenemos la verdadera magnitud 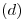 del segmento
del segmento  , que es lo que nos habían pedido.
, que es lo que nos habían pedido.
Discusión
 .
. : esto no significa para nada que el plano
: esto no significa para nada que el plano  esté en una posición muy peculiar. De hecho, si uno releva el plano
esté en una posición muy peculiar. De hecho, si uno releva el plano 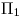 (que, recordemos, se ha abatido sobre el
(que, recordemos, se ha abatido sobre el 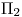 ), y se imagina el plano
), y se imagina el plano  con sus trazas así como las indica el dibujo, no aparenta estar en ninguna posición demasiado interesante.
con sus trazas así como las indica el dibujo, no aparenta estar en ninguna posición demasiado interesante.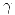 (sobre el icnográfico) y la recta de su intersección con
(sobre el icnográfico) y la recta de su intersección con  son innecesarios, en principio, pero pueden servir de control, de que el punto
son innecesarios, en principio, pero pueden servir de control, de que el punto 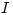 hallado sea el correcto.
hallado sea el correcto.
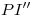 en lugar de hacerlo con radio
en lugar de hacerlo con radio  .
.