Tabla de Contenidos
Examen Parcial - 70.03. Medios de Representación "A" - 29/06/2007
Cátedra: Curso 002 — Botet – Sande – Vergez
Fecha: 1° Oportunidad - 1° Cuatrimestre 2007
Día: 29/06/2007
Enunciado
Datos:

 .
.
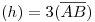 .
.
Hoja de Datos (en formato dwg)
Hallar:
 .
.
 .
.
Resolución
- Hallar la icnografía de
 : Para ello prolongamos el segmento
: Para ello prolongamos el segmento 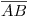 hasta la línea de tierra, y bajamos ese punto (
hasta la línea de tierra, y bajamos ese punto ( ) hasta
) hasta 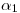 para hallar
para hallar 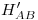 . Necesitamos otro punto de la icnografía. Entonces trazamos una horizontal del plano pasante por
. Necesitamos otro punto de la icnografía. Entonces trazamos una horizontal del plano pasante por  (
(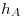 ), y en la intersección de
), y en la intersección de  con una vertical trazada por
con una vertical trazada por 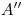 tenemos
tenemos 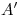 . Por allí, y partiendo de
. Por allí, y partiendo de 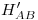 , trazamos
, trazamos 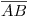 , sobre la cual encontramos
, sobre la cual encontramos 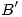 del mismo modo que lo hicmos para
del mismo modo que lo hicmos para 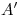 .
. - Hallar la icnografía del cuadrado que es base de la pirámide: Para ello haremos uso de un abatimiento de
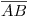 sobre el icnográfico, eligiendo como eje a
sobre el icnográfico, eligiendo como eje a  .
. 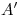 coincidirá pues con
coincidirá pues con 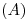 . En cuanto a
. En cuanto a  , medimos su altura respecto de
, medimos su altura respecto de 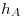 , en definitiva, la de
, en definitiva, la de 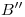 respecto de
respecto de 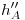 . Luego, para encontrar
. Luego, para encontrar 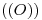 , medimos dicha distancia sobre
, medimos dicha distancia sobre 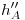 y a partir de
y a partir de 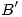 en uno cualquiera de los dos sentidos posibles. Trazamos una perpendicular a
en uno cualquiera de los dos sentidos posibles. Trazamos una perpendicular a  pasante por
pasante por 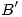 , y en la intersección de ambas clavamos el compás. Con extremo en
, y en la intersección de ambas clavamos el compás. Con extremo en 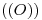 , trazamos un arco de circunferencia, hasta cortar a esa perpendicular más allá de
, trazamos un arco de circunferencia, hasta cortar a esa perpendicular más allá de  . Hemos encontrado
. Hemos encontrado 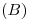 , y uniéndolo con
, y uniéndolo con  obtenemos
obtenemos  . Ahora sólo debemos trazar un cuadrado de lado
. Ahora sólo debemos trazar un cuadrado de lado  . Para relevar
. Para relevar  , lo prolongamos hasta el eje, y por esta intersección y por
, lo prolongamos hasta el eje, y por esta intersección y por 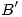 trazamos
trazamos 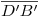 hasta que intersecte a una perpendicular al eje pasante por
hasta que intersecte a una perpendicular al eje pasante por  . Acabamos de encontrar
. Acabamos de encontrar 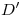 , y para terminar con esta parte de la resolución, trazamos otra perpendicular a
, y para terminar con esta parte de la resolución, trazamos otra perpendicular a  , pero pasante por
, pero pasante por  , y trazamos también una paralela a
, y trazamos también una paralela a 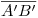 pasante por
pasante por 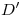 . En la intersección de ambas tenemos
. En la intersección de ambas tenemos 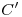 , y podemos por fin completar con segmentos la icnografía de la base de la pirámide. Si hasta ahora hemos hecho todo correctamente,
, y podemos por fin completar con segmentos la icnografía de la base de la pirámide. Si hasta ahora hemos hecho todo correctamente, 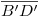 debería ser paralela a
debería ser paralela a 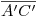 .1)
.1) - Hallar la ortografía del cuadrado que es base de la pirámide: Para subir
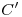 utilizamos una frental
utilizamos una frental 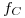 perteneciente a
perteneciente a  y pasante por
y pasante por  , y en la intersección de
, y en la intersección de 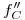 con una vertical trazada por
con una vertical trazada por 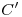 hallamos
hallamos 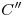 .2) Para subir
.2) Para subir 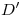 hacemos uso de una horizontal
hacemos uso de una horizontal 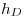 perteneciente a
perteneciente a  y pasante por
y pasante por  , y en la intersección de
, y en la intersección de 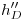 con una vertical trazada por
con una vertical trazada por 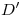 hallamos
hallamos 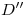 . Completamos la ortografía con segmentos, controlando que
. Completamos la ortografía con segmentos, controlando que 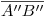 sea paralelo a
sea paralelo a 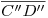 , y que
, y que  sea paralelo a
sea paralelo a 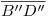 . Como en la próxima sección habremos de necesitar al centro
. Como en la próxima sección habremos de necesitar al centro 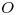 de la base piramidal, antes de terminar ésta, lo hallaremos: trazamos dos diagonales del cuadrilátero
de la base piramidal, antes de terminar ésta, lo hallaremos: trazamos dos diagonales del cuadrilátero  y en su intersección encontramos
y en su intersección encontramos 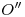 . Por él bajamos una vertical hasta que intersecte a la diagonal
. Por él bajamos una vertical hasta que intersecte a la diagonal 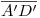 y entonces encontramos a
y entonces encontramos a  .
. - Completar la Pirámide: Primero debemos trazar la normal
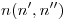 al plano
al plano  pasante por
pasante por 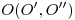 . Una vez hecho esto, tenemos que hacer una de tres cosas (abatir, girar o cambiar de planos) para poder medir sobre
. Una vez hecho esto, tenemos que hacer una de tres cosas (abatir, girar o cambiar de planos) para poder medir sobre  la altura que es
la altura que es 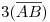 . Por comodidad, giraremos la normal en torno a un eje perpendicular al plano icnográfico: primero, elegimos un punto
. Por comodidad, giraremos la normal en torno a un eje perpendicular al plano icnográfico: primero, elegimos un punto 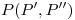 cualquiera perteneciente a
cualquiera perteneciente a  , y con extremo en
, y con extremo en 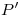 , apoyando el compás en
, apoyando el compás en  , trazamos un arco de circunferencia en sentido horario hasta intersectar a una horizontal trazada por
, trazamos un arco de circunferencia en sentido horario hasta intersectar a una horizontal trazada por  . Esta horizontal es, en realidad,
. Esta horizontal es, en realidad, 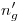 , y la intersección que acabamos de encontrar viene siendo
, y la intersección que acabamos de encontrar viene siendo 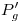 . Por este punto levantamos una vertical, y por
. Por este punto levantamos una vertical, y por 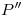 una horizontal: donde se intersectan está
una horizontal: donde se intersectan está 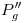 . Uniendo este punto con
. Uniendo este punto con 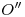 tenemos
tenemos 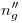 . Sobre ella encontramos
. Sobre ella encontramos 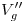 , a una distancia
, a una distancia 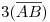 de
de 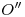 , siendo
, siendo  el vértice de la pirámide. A
el vértice de la pirámide. A 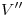 se lo encuentra simplemente en la intersección de
se lo encuentra simplemente en la intersección de 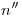 con una horizontal trazada por
con una horizontal trazada por 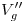 . A
. A 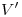 se lo encuentra también facilmente, en consecuencia, en la intersección de
se lo encuentra también facilmente, en consecuencia, en la intersección de 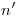 con una vertical trazada por
con una vertical trazada por 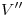 .3) Ahora que tenemos
.3) Ahora que tenemos 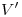 , la icnografía de la pirámide se puede competar uniéndolo con
, la icnografía de la pirámide se puede competar uniéndolo con 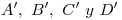 . Y ahora que tenemos
. Y ahora que tenemos 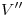 , la ortografía piramidal se puede completar uniéndolo con
, la ortografía piramidal se puede completar uniéndolo con 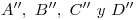 .
.
En lo que a visibilidad respecta, los contornos aparentes icnográfico y ortográfico son desde ya visibles: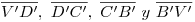 , y
, y 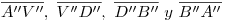 . Los únicos segmentos conflictivos son entonces: (en icnografía)
. Los únicos segmentos conflictivos son entonces: (en icnografía) 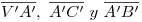 , y (en ortografía)
, y (en ortografía) 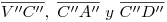 . Para la icnografía es preciso observar que: si la elevación de
. Para la icnografía es preciso observar que: si la elevación de  es mayor que la de
es mayor que la de  ,
, 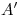 será visible, y viceversa. Concluimos entonces (con sólo mirar la ortografía) que
será visible, y viceversa. Concluimos entonces (con sólo mirar la ortografía) que 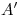 es invisible. Para la ortografía es menester observar que: si el alejamiento de
es invisible. Para la ortografía es menester observar que: si el alejamiento de  es mayor que el de
es mayor que el de  ,
, 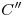 será visible, y viceversa. Concluimos entonces (con sólo mirar la icnografía) que
será visible, y viceversa. Concluimos entonces (con sólo mirar la icnografía) que 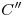 es invisible. Si hasta ahora hemos hecho todo bien, nuestra nota es un 4 (cuatro).
es invisible. Si hasta ahora hemos hecho todo bien, nuestra nota es un 4 (cuatro). - Obtener la sección con
 : Como
: Como 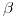 es paralelo al plano ortográfico, id est, proyectante sobre el icnográfico, la icnografía de la sección coincidirá con
es paralelo al plano ortográfico, id est, proyectante sobre el icnográfico, la icnografía de la sección coincidirá con 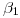 y será un segmento limitado por
y será un segmento limitado por  y por
y por  . A las intersecciones de ese segmento con
. A las intersecciones de ese segmento con 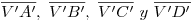 las podemos subir a
las podemos subir a 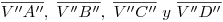 , respectivamente, obteniendo el cuadrilátero que es ortografía de la sección de la pirámide con el plano
, respectivamente, obteniendo el cuadrilátero que es ortografía de la sección de la pirámide con el plano 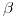 dado. En lo que respecta a la visibilidad del mismo,
dado. En lo que respecta a la visibilidad del mismo, 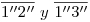 no serán visibles pues se encuentran sobre caras invisibles del cuerpo en cuestión, mientras que (por una razón análoga) sí son visibles los segmentos
no serán visibles pues se encuentran sobre caras invisibles del cuerpo en cuestión, mientras que (por una razón análoga) sí son visibles los segmentos  .
.
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
1)
Nótese pues que podríamos haber procedido al revés, haber trazado una paralela a 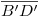 por
por 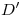 , y hacer este control con ayuda de una paralela a
, y hacer este control con ayuda de una paralela a 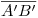
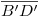 por
por 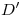 , y hacer este control con ayuda de una paralela a
, y hacer este control con ayuda de una paralela a 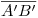
2)
Después de tantas escrituras y borradas, al final olvidé poner nomenclatura a 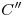 , pero creo que aún se notan las marcas de escrituras anteriores.
, pero creo que aún se notan las marcas de escrituras anteriores.
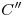 , pero creo que aún se notan las marcas de escrituras anteriores.
, pero creo que aún se notan las marcas de escrituras anteriores.3)
A modo de control se puede trazar una vertical por 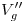 hasta cortar a
hasta cortar a 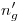 , luego un arco de circunferencia con centro en
, luego un arco de circunferencia con centro en  y extremo en
y extremo en 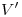 hasta cortar a
hasta cortar a 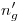 , y ver que ambas intersecciones coincidan.
, y ver que ambas intersecciones coincidan.
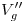 hasta cortar a
hasta cortar a 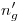 , luego un arco de circunferencia con centro en
, luego un arco de circunferencia con centro en  y extremo en
y extremo en 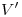 hasta cortar a
hasta cortar a 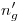 , y ver que ambas intersecciones coincidan.
, y ver que ambas intersecciones coincidan.Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported

