Tabla de Contenidos
70.03 Medios de Representación "A" - Ejercicio - Cuerpos y Secciones Planas
Período: 1er Cuatrimestre 2007
Curso: 002 — Botet - Sande - Vergez.
Ejercicio
Enunciado
Datos:
 .
.
 .
.
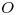 es centro de la base de un cilindro recto, R = 3 cm, h = 10 cm.
es centro de la base de un cilindro recto, R = 3 cm, h = 10 cm.
Hallar:
Cilindro.
Sección con 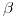 .
.
Resolución
- Encontrar
 : se traza una horizontal
: se traza una horizontal 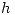 que pertenezca a
que pertenezca a  y tal que
y tal que 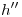 pase por
pase por 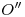 .
.  se encuentra en la intersección de
se encuentra en la intersección de  con una vertical trazada por
con una vertical trazada por 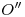 .
. - Trazar las elipses que son base del cilindro: sobre la horizontal, en ambos sentidos desde
 , se mide el radio R dado. Se determinan así
, se mide el radio R dado. Se determinan así 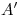 y
y 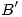 , extremos del diámetro mayor de la elipse. Para encontrar el diámetro menor, determinado por los puntos
, extremos del diámetro mayor de la elipse. Para encontrar el diámetro menor, determinado por los puntos 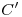 y
y 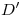 , se procede como sigue. Eligiéndose
, se procede como sigue. Eligiéndose 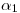 como eje de abatimiento, se traza una perpendicular a
como eje de abatimiento, se traza una perpendicular a  por
por  , que será a su vez la traza icnográfica
, que será a su vez la traza icnográfica  de la recta de máxima pendiente
de la recta de máxima pendiente  del plano
del plano  . Se abate
. Se abate  y con centro en
y con centro en 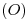 se traza una circunferencia de radio R. Los puntos
se traza una circunferencia de radio R. Los puntos  y
y  se hallan en la intersección de la circunferencia con
se hallan en la intersección de la circunferencia con 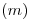 , abatimiento de la recta de máxima pendiente del plano
, abatimiento de la recta de máxima pendiente del plano  . Para encontrar
. Para encontrar 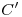 y
y 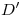 , se relevan1)
, se relevan1)  y
y  , respectivamente. Los puntos
, respectivamente. Los puntos 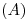 y
y 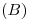 se hallan, por supuesto, en la intersección de paralelas a
se hallan, por supuesto, en la intersección de paralelas a 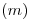 trazadas desde
trazadas desde  y
y  , respectivamente (si no es así, evidentemente se ha cometido un error). Alternativamente, para encontrar
, respectivamente (si no es así, evidentemente se ha cometido un error). Alternativamente, para encontrar 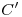 y
y 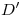 , también se puede medir sobre
, también se puede medir sobre  el radio R, con lo cual se obtiene
el radio R, con lo cual se obtiene  . Para hallar
. Para hallar 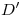 se interseca a
se interseca a  con una paralela a
con una paralela a  trazada por
trazada por  . La posición de
. La posición de 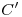 es inmediata ya que
es inmediata ya que  . Así encontrados
. Así encontrados 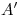 ,
, 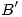 ,
, 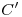 y
y 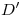 , se puede trazar la elipse de diámetros perpendiculares, icnografía de la circunferencia base del cilindro.
, se puede trazar la elipse de diámetros perpendiculares, icnografía de la circunferencia base del cilindro.
Para hallar la traza ortográfica de dicha circunferencia se levantan verticales desde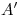 y
y 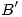 , y se encuentra su intersección con
, y se encuentra su intersección con 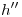 (recordar que
(recordar que  y
y  pertenecen a
pertenecen a 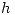 ). Acto seguido, se encuentra
). Acto seguido, se encuentra 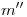 , levantando una vertical desde
, levantando una vertical desde 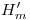 (intersección de
(intersección de 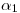 con
con  ) hasta la línea fundamental – lo que da
) hasta la línea fundamental – lo que da  – y otra vertical, desde
– y otra vertical, desde  (intersección de la línea de tierra con
(intersección de la línea de tierra con  ) hasta
) hasta 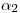 – lo que da
– lo que da  . Se levantan entonces dos verticales más, esta vez desde
. Se levantan entonces dos verticales más, esta vez desde 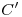 y desde
y desde 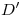 , para encontrar, en su intersección con
, para encontrar, en su intersección con 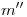 ,
, 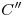 y
y 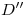 , respectivamente. Quedan así determinados los dos diámetros conjugados, mayor y menor, de la elipse.
, respectivamente. Quedan así determinados los dos diámetros conjugados, mayor y menor, de la elipse. - Hallar las trazas del eje del cilindro y las dos elipses restantes: se trazan
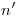 y
y 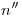 , respectivamente perpendiculares a
, respectivamente perpendiculares a 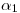 y a
y a 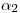 y pasantes por
y pasantes por  y
y 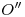 . Para obtener la verdadera magnitud del eje en icnografía, se procede a girar la recta
. Para obtener la verdadera magnitud del eje en icnografía, se procede a girar la recta  en torno de un eje de giro
en torno de un eje de giro 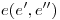 perpendicular al plano ortográfico y que pasa por
perpendicular al plano ortográfico y que pasa por 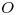 . Se elige para ello un punto cualquiera de
. Se elige para ello un punto cualquiera de  , llamémoslo (en un rapto de originalidad)
, llamémoslo (en un rapto de originalidad)  : se marcan
: se marcan 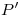 y
y 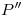 sobre
sobre 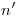 y
y 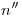 respectivamente. Se traza, con centro en
respectivamente. Se traza, con centro en 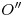 y extremo en
y extremo en 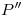 , un arco de circunferencia en sentido antihorario, de manera que
, un arco de circunferencia en sentido antihorario, de manera que 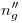 resulte paralela a la línea de tierra. En la intersección de una vertical trazada desde
resulte paralela a la línea de tierra. En la intersección de una vertical trazada desde 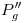 y una horizontal trazada desde
y una horizontal trazada desde 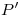 se encuentra
se encuentra 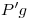 , determinándose (junto con
, determinándose (junto con 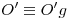 )
) 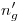 . Ahora, sobre
. Ahora, sobre 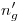 se mide la altura h dada, y se marca el punto
se mide la altura h dada, y se marca el punto 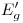 . Levantando una vertical por dicho punto se encuentra
. Levantando una vertical por dicho punto se encuentra 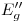 sobre
sobre 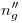 . Ahora se procede a girar en sentido horario, con centro en
. Ahora se procede a girar en sentido horario, con centro en  y extremo en
y extremo en 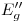 , hasta encontrar
, hasta encontrar 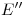 en la intersección del arco con
en la intersección del arco con 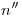 . Se baja una vertical desde este punto hasta
. Se baja una vertical desde este punto hasta 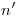 para encontrar
para encontrar 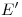 . Queda así determinado el eje del cilindro.
. Queda así determinado el eje del cilindro.
Por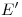 se traza una paralela a
se traza una paralela a  y sobre ella, en ambos sentidos, se mide la distancia
y sobre ella, en ambos sentidos, se mide la distancia 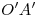 , determinándose el diámetro mayor de la tercera elipse, de extremos
, determinándose el diámetro mayor de la tercera elipse, de extremos 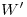 y
y 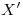 . Se traza también por
. Se traza también por 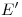 una paralela a
una paralela a  , midiéndose en ambos sentidos sobre la misma la distancia
, midiéndose en ambos sentidos sobre la misma la distancia 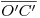 , para determinar así el diámetro menor, cuyos extremos son
, para determinar así el diámetro menor, cuyos extremos son 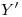 y
y 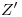 . Esta elipse resulta idéntica a la primera por ser paralelos los dos planos que forman, uno la base, y otro el extremo, del cilindro.
. Esta elipse resulta idéntica a la primera por ser paralelos los dos planos que forman, uno la base, y otro el extremo, del cilindro.
Para hallar la cuarta elipse, ortografía de la circunferencia extremo del cilindro, se procede de manera similar: por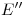 se traza una paralela a
se traza una paralela a 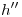 , y se lleva sobre ella el segmento
, y se lleva sobre ella el segmento 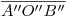 , encontrándose su diámetro mayor
, encontrándose su diámetro mayor 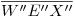 . Se traza luego por aquel punto también una paralela a
. Se traza luego por aquel punto también una paralela a 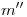 , llevándose sobre esta el segmento
, llevándose sobre esta el segmento 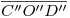 , quedando determinado el diámetro menor
, quedando determinado el diámetro menor 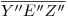 . Si hasta ahora se ha hecho lo correcto, bajándose verticales desde
. Si hasta ahora se ha hecho lo correcto, bajándose verticales desde 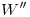 ,
, 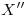 ,
, 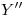 y
y 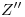 se deben encontrar
se deben encontrar 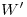 ,
, 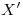 ,
, 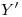 y
y 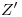 , respectivamente. Esta cuarta elipse debe ser idéntica a la segunda, análogamente a lo sucedido con la tercera y la primera.
, respectivamente. Esta cuarta elipse debe ser idéntica a la segunda, análogamente a lo sucedido con la tercera y la primera. - Completar el cuerpo: una vez trazadas las cuatro elipses, se completa el contorno aparente del cuerpo con líneas paralelas a
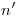 (en icnografía) y
(en icnografía) y 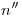 (en ortografía), tangentes a dichas curvas. Los puntos de tangencia en ortografía de estas líneas se fijan por la intersección con las elipses segunda y cuarta de un segmento normal a
(en ortografía), tangentes a dichas curvas. Los puntos de tangencia en ortografía de estas líneas se fijan por la intersección con las elipses segunda y cuarta de un segmento normal a 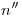 pasante por
pasante por 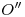 y
y 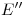 , respectivamente. Dichos puntos son
, respectivamente. Dichos puntos son  ,
, 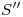 ,
, 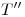 y
y 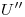 . Determinemos ahora la visibilidad.
. Determinemos ahora la visibilidad.
En ortografía, el contorno aparente lo forma la unión de: el arco , las dos paralelas a
, las dos paralelas a 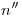 tangentes a las elipses segunda y cuarta, y el arco
tangentes a las elipses segunda y cuarta, y el arco 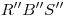 . Si el arco
. Si el arco 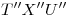 es visible, debe observarse en icnografía que
es visible, debe observarse en icnografía que 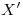 se encuentra delante de
se encuentra delante de 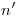 (tomando como punto de referencia al
(tomando como punto de referencia al  ). Idéntica consideración es válida para el arco
). Idéntica consideración es válida para el arco  . Resulta entonces que el primero es visible (y se dibuja por tanto en línea llena) y el segundo no lo es (y se dibuja por lo tanto en línea de trazos).
. Resulta entonces que el primero es visible (y se dibuja por tanto en línea llena) y el segundo no lo es (y se dibuja por lo tanto en línea de trazos).
En cuanto a la icnografía, el contorno aparente lo forma la unión de: el arco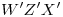 , las dos paralelas a
, las dos paralelas a 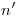 tangentes a las elipses primera y tercera, y el arco
tangentes a las elipses primera y tercera, y el arco 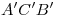 . Si el arco
. Si el arco  es visible, debe observarse en ortografía que
es visible, debe observarse en ortografía que 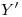 está arriba de
está arriba de 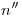 (tomando como punto de referencia al
(tomando como punto de referencia al  ). Idéntica consideración es válida para el arco
). Idéntica consideración es válida para el arco  . Resulta entonces que el primero es visible (y se dibuja en línea llena), y el segundo no (dibujándose en línea de trazos). Quedan así completas las dos proyecciones del cuerpo.
. Resulta entonces que el primero es visible (y se dibuja en línea llena), y el segundo no (dibujándose en línea de trazos). Quedan así completas las dos proyecciones del cuerpo. - Sección con
 : Siendo
: Siendo 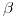 un plano proyectante sobre
un plano proyectante sobre 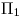 , la icnografía de su intersección con el cilindro será una línea coincidente con
, la icnografía de su intersección con el cilindro será una línea coincidente con 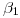 . Los puntos en ortografía, intersección de ambas superficies, pueden ser fácilmente encontrados levantando verticales desde sus correspondientes en icnografía (todos estos últimos se encontrarán, por supuesto, sobre
. Los puntos en ortografía, intersección de ambas superficies, pueden ser fácilmente encontrados levantando verticales desde sus correspondientes en icnografía (todos estos últimos se encontrarán, por supuesto, sobre 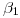 ). En este caso, la intersección resulta ser un cuadrilátero curvilíneo (el
). En este caso, la intersección resulta ser un cuadrilátero curvilíneo (el  ), siendo
), siendo 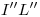 y
y 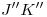 arcos elípticos, por ser
arcos elípticos, por ser 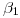 no paralelo a
no paralelo a 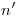 .
.
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
1)
lo contrario de 'se abaten', o de 'se rebaten'
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported

