Parte escrita del final de Hidráulica General del 03 de marzo de 2008. Lugo de resolver estos problemas comienza la parte oral donde se puede preguntar sobre todos los temas.
- Diseñar un canal de sección trapecial de pendiente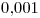 
con material de tierra vegetal compacta para un caudal de 
que sea de máxima eficiencia.
- Calcular las perdidas que tiene un conducto a presión de
hecho de PVC de 
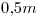de diametro y un caudal de 
. - Describir lo que es la red de escurrimiento, formulas básicas, modos de utlizarla, ejemplos sencillos, etc.
Al ser de tierra vegetal compacta se utiliza, un 
si la altura es menor a un metro y
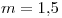si es mayor a un metro. El n de Manning es aproximadamente 
. Para máxima eficiencia se útiliza la fórmula 
que proviene de mínimizar el périmetro mojado con un 
y una sección constante.
Pruebo primero con y como resultado obtengo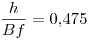 
. Busco este número en la tabla Woodward y Posey junto al talud ya fijado obtego que 
.
Por lo tanto, se obtiene un canal de tirante 
y una base de fondo de 
que cumple con lo pedido.
Averiguo primero el número de Reynolds 
.
Tomando al PVC como un material casi liso que respeta muy bien la linea de tuberías lisas del abaco universal, busco en el mismo, el valor de 
y luego utilizando la ecuación de Darcy, hallo las pérdidas a lo largo de toda la tubería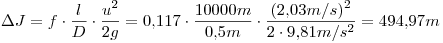 
que es lo que se pedía.
