Final - 67.52. Termodinámica B - 16/07/2012
Cátedra: Coladonato
Fecha: 2do Final - Invierno 2012
Día: 16/07/2012
Enunciado
Parte Práctica
Una masa de aire húmedo, a 20ºC y 50% de humedad relativa, circula por un conducto adiabático y debe ser llevada a 30ºC y 70% de humedad relativa, mediante los siguientes procesos sucesivos:
- Calentamiento con resistencia eléctrica
- Humidificación con agua a 0ºC, hasta 100% de humedad relativa
- Calentamiento posterior con resistencia eléctrica
Si el proceso se realiza a pt = 1atm (101,33 KPa), siendo la masa de aire seco de 500kg/hora, graficar los procesos en un esquema del diagrama de Mollier y determinar analíticamente:
- Masa de aire húmedo inicial.
- Calor total suministrado.
- Masa de agua agregada.
- Masa de aire húmedo final.
Datos:
- x=0,622.pv/(pt-pv)
- h=cpas.t+x.(r0+cpv.t)
- cpas=1,006 KJ/Kh.ºK
- cpv=1,863 KJ/Kg.ºK
- r0=2501,59 KJ/Kg
- Ras=0,2868 KJ/Kg.ºK
- Rv=0,4613 KJ/Kg.ºK
Parte Teórica
Punto 1
En una cámara rígida y adiabática, se mezclan 2 corrientes de agua a las mismas condiciones de presión y temperatura, una de líquido saturado y otra de vapor saturado. ¿Cuánto vale la variación de entropía del universo?
Punto 2
En un ciclo de vapor, el líquido saturado a la salida del condensador, entra a una bomba adiabática de rendimiento isoentrópico = 1 y es comprimido hasta la presión de la caldera. Representar en un esquema del diagrama T-S la evolución y determinar analíticamente el trabajo de la bomba y la entalpía del líquido a la salida de la misma.
Punto 3
Instalación frigorífica a régimen seco con subenfriamiento. Esquema y ciclo en el diagrama logP-h.
Punto 4
En la instalación anterior, el coeficiente de efecto frigorífico es <1, =1 o >1?
Punto 5
Si un aire húmedo es comprimido a t=cte, ¿cómo varía su humedad relativa?
Resolución
Parte Práctica
 se mantiene constante a lo largo de todo el ejercicio, pues no se agrega más aire en ninguna etapa.
se mantiene constante a lo largo de todo el ejercicio, pues no se agrega más aire en ninguna etapa.
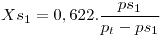
Teniendo  , saco de la tabla
, saco de la tabla  y hallo
y hallo 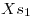
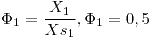
De la formula anterior hallo 

De la formula anterior hallo 
Ya se puede responder el primer punto. Masa de aire húmedo inicial: 
Al calentar por primera vez  , con
, con 
Por lo tanto  (1)
(1)
Al humidificar  (2)
(2)
Y también 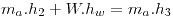 (3)
(3)
Al volver a calentar 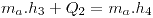 (4)
(4)
Tengo la temperatura en el punto 4,  . Busco en la tabla el valor de
. Busco en la tabla el valor de 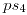

De la ecuación anterior hallo 

De la ecuación anterior hallo 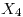
Teniendo 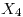 y
y 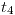 , hallo
, hallo 
 y
y  pues en esos procesos no se agrega o quita agua ni aire
pues en esos procesos no se agrega o quita agua ni aire
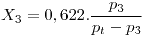
Resuelvo la ecuación anterior para hallar 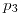
Debido a que en el punto 3 el aire húmedo está con  (saturado), voy a la tabla y busco el valor de la temperatura a esa presión. Hallo
(saturado), voy a la tabla y busco el valor de la temperatura a esa presión. Hallo 
Teniendo  y
y  , hallo
, hallo 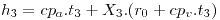
De la ecuación (2), teniendo en cuenta que  y
y  hallo
hallo  , que es la tercer cosa que nos piden
, que es la tercer cosa que nos piden
De la ecuación (3) se llega a la conclusión de que  . Esto se debe a que por estar el agua a 0ºC,
. Esto se debe a que por estar el agua a 0ºC, 
Dispongo de  y
y  , por lo tanto calculo
, por lo tanto calculo 
De la ecuación (1) (teniendo en cuenta que ya conozco 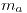 ,
,  y
y 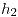 ) obtengo
) obtengo 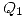
Respondo la segunda pregunta: 
Respondo la cuarta pregunta: 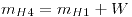
Parte Teórica
Punto 1

 pues la cámara es rígida y adiabática, por lo tanto no interacciona con el medio.
pues la cámara es rígida y adiabática, por lo tanto no interacciona con el medio.
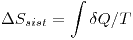
Al estar los dos fluidos a la misma temperatura, no intercambian calor. Y si lo hicieran, lo que libera uno lo absorve el otro, por lo tanto 
Se concluye que 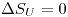
Punto 2


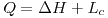
 pues la bomba es adiabática
pues la bomba es adiabática


También sé que 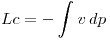
Si considero que el volumen específico del líquido es constante:

Por lo tanto del siguiente sistema de ecuaciones hallamos el trabajo de la bomba y la entalpía a la salida de la bomba.

Punto 3
Punto 4
ε>1
Punto 5
Xs=0,662.pvs/(pt-pvs)
Si ↑ pt, ↓ Xs
Si ↓ pt, ↑ Xs
φ=X/Xs
Si ↑ pt, ↑ φ
Si ↓ pt, ↓ φ


