Examen Parcial - 67.16. Ensayos Industriales - 11/06/2007
Cátedra: Única (Svoboda-Blangino)
Fecha: 1º Oportunidad - 1º Cuatrimestre 2007
Día: 11/06/2007
Enunciado
Punto 1
Compuestos. Análisis por isotensión e isodeformación. Influencia de la orientación. Fibras cortas.
Punto 2
Ensayo de compresión. Ventajas. Limitaciones. Correcciones. Ensayo de Watts y Ford.
Punto 3
Se desea saber el momento torsor necesario para que una barra de sección circular de d=20 mm de cierto material entre en fluencia, sabiendo que los resultados del ensayo de tracción para el material son: Pf = 72.500 N, Δlestric = 38 mm, D0 = 20 mm, L0 = 100 mm. Además, se desea endurecer el material para que soporte 270 MPa en torsión. Se dispone de una máquina para endurecer el material mediante deformación con una capacidad máxima de 750 Nm. ¿Es posible utilizar esta máquina?
Punto 4
Durante la unión de dos recipientes a presión se desarrolló una fisura a lo largo de todo el perímetro del recipiente y de profundidad igual a 1/8 del espesor de la pared. El diámetro del recipiente (externo) es 1000 mm y el espesor de la pared e = 20 mm. Se sabe que el KIC = 20 MPa m½ y la tensión de fluencia σy = 850 MPa. Calcular la presión de rotura. ¿La falla se produce por colapso plástico o por fractura rápida?.
Punto 5
Ensayo Charpy. Objetivos. Procedimiento. Resultados obtenidos. Alcance del ensayo.
Resolución
Punto 3
Considerando el criterio de Von Mises:


La fluencia se va a dar para 
Como 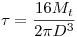 , entonces la fluencia se va a dar para
, entonces la fluencia se va a dar para  .
.
Por lo tanto: 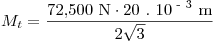
Mt = 418,58 Nm
Otra forma, usando el criterio de Tresca, 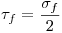 Entonces:
Entonces: 
Mt = 362,5 Nm
La tensión última de corte es: 
Entonces, 
Resulta: Mt = 564,49 Nm
Como Mtu < Mtmax, SÍ se puede utilizar el equipo.
Punto 4
La tensión que actúa sobre la fisura en modo I de apertura es la σzz.
Por equilibrio de fuerzas: 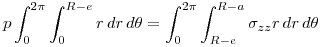 .
.
Como es un recipiente de pared delgada  , se puede suponer σzz uniforme en el espesor.
, se puede suponer σzz uniforme en el espesor.
Entonces:

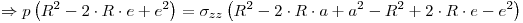
Cancelando términos, y despreciando e2 y a2 por ser valores pequeños:
∴ 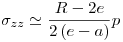
Según la MFLE1), la falla se dispara cuando KIaplic = KIC.
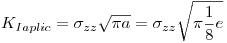
Entonces, 
Finalmente, resulta: 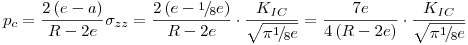

pc = 17,17 MPa
Se puede calcular el valor de la tensión, que es σzz = 225,66 MPa.
Nuevamente el equilibrio de fuerzas, ahora en la dirección circunferencial:
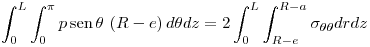
![<tex>p \cdot \left( {R - e} \right) \cdot 2L = 2\sigma _{\theta \theta } \left[ {\left( {R - a} \right) - \left( {R - e} \right)} \right] \cdot L</tex> <tex>p \cdot \left( {R - e} \right) \cdot 2L = 2\sigma _{\theta \theta } \left[ {\left( {R - a} \right) - \left( {R - e} \right)} \right] \cdot L</tex>](lib/plugins/latex/images/6a5ffed4f3223d1be971c2bc8307c594e2bf6357_0.png)
∴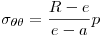 .
.
Esta tensión resulta σθθ = 470,95 MPa.
Por último, 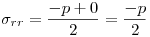 es el valor medio de tensión radial, despreciable frente a las otras que son mucho mayores. (σrr = – 8,59 MPa).
es el valor medio de tensión radial, despreciable frente a las otras que son mucho mayores. (σrr = – 8,59 MPa).
Usando el criterio de Von Mises para terna principal:

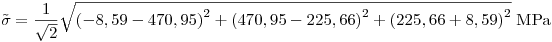
Como  < σy = 850 MPa, la falla se da por fractura rápida (se dispara la fisura) y no por fluencia (colapso plástico).
< σy = 850 MPa, la falla se da por fractura rápida (se dispara la fisura) y no por fluencia (colapso plástico).
