Parcial - 66.74. Señales y Sistemas
Cátedra: Todas
Fecha: 2da Oportunidad - 1er Cuatrimestre 2007
Día: 11/06/2007
Enunciado
Punto I
Sea un sistema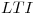 
cuya respuesta al impulso es una dada 
, y que para una entrada particular 
(acotada) su salida es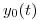 
como se muestra en el siguiente gráfico:
, y sistemas 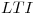determinados por su correspondiente respuesta al impulso, 
:
; 
.
; .
; 
.
; .- ;
. 
; .
; 
.
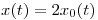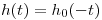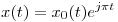Se pide para cada uno de los casos anteriores, determinar si hay información suficiente para encontrar la salida 
correspondiente, y en caso de que la haya, graficar dicha salida, indicando sus valores relevantes.
Punto II
Cuando la entrada a un sistema 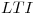causal es:
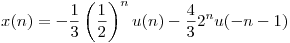
la transformada Z de la salida es:
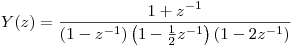
- ¿Cuál es la región de covergencia de
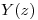? - Encontrar la respuesta al impulso
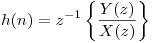del sistema. ¿Es estable? - Encontrar la ecuación en diferencias que representa a este sistema indicando la condición inicial.
Punto III
La señal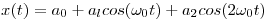 
es muestreada con una frecuencia de muestreo dada por 
, obteniéndose de este modo una señal de tiempo discreto 
.
- Encuentre la expresión de y de su tranformada de Fouríer,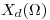
. Graficar el espectro encontrado, indicando puntos relevantes y amplítudes. ¿Es periódica (justifique su respuesta)? - Sea ahora
para 
y 0 en el resto. Se obtiene la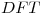 
de 5 puntos de dicha señal, obteniéndose ![<tex>X_v(k) =[5 \ 2 \ 3 \ a \ b]</tex>](lib/plugins/latex/images/6235d959502f582ae2689d2088f18d00d8a54e39_0.png "<tex>X_v(k) =[5 \ 2 \ 3 \ a \ b]</tex>")
.Encontrar los valores de 
, 
y de 
, 
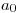y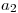 
·
Resolución
Punto I
1. ; 
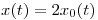2. 
3. ; .
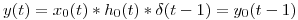
4. ; .
Es este caso para encontrar se deberían conocer e 
.
5. ; .
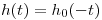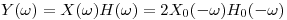
Sea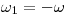 
: 
6. ; .
![<tex>Y(\omega)=X(\omega)H(\omega)=\frac{1}{2\pi}\{X_0(\omega)*[\pi(\delta(\omega-\pi)+\delta(\omega+\pi))]\}H_0(\omega)</tex>](lib/plugins/latex/images/73f5dc5e2b6e1a9d21cb047234aca24cd11aef59_0.png "<tex>Y(\omega)=X(\omega)H(\omega)=\frac{1}{2\pi}\{X_0(\omega)*[\pi(\delta(\omega-\pi)+\delta(\omega+\pi))]\}H_0(\omega)</tex>")
Antitransformando:
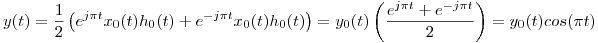
7. ; .
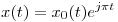Es este caso para encontrar se deberían conocer e .
