Parcial - 66.74. Señales y Sistemas
Cátedra: Todas
Fecha: 1er Oportunidad - 1er Cuatrimestre 2007
Día: 28/05/2007
Enunciado
Punto I
Para el sistema que se muestra en la figura siguiente:

en el cual 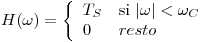 es un filtro pasabajos ideal y
es un filtro pasabajos ideal y  es una señal de banda limitada en
es una señal de banda limitada en  . Se pide:
. Se pide:
- Encontrar las transformadas de Fourier de las señales
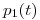 y
y  y graficarlas, indicando amplitudes y puntos relevantes.
y graficarlas, indicando amplitudes y puntos relevantes. - Encontrar las transformadas de Fourier de las señales
 ,
,  y
y  para una
para una  genérica que cumpla la especificación pedida.
genérica que cumpla la especificación pedida. - Cuál es el valor (o rango de valores) que puede tomar
 para que
para que  pueda ser recuperado a partir de
pueda ser recuperado a partir de  ?
? - Cuál es el valor que debe tomar
 del filtro
del filtro  para que
para que  ? Dibujar
? Dibujar  para dicho caso (considere que se cumple lo especificado en el punto anterior).
para dicho caso (considere que se cumple lo especificado en el punto anterior).
Punto II
Sea un sistema 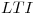 definido por su respuesta en frecuencia
definido por su respuesta en frecuencia  , cuya entrada es la secuencia
, cuya entrada es la secuencia  ,
,  y cero para todo otro
y cero para todo otro  . Se pide
. Se pide
- Determinar la salida
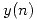 del sistema y graficarla.
del sistema y graficarla. - Hallar
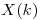 , la
, la 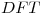 de
de 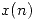 , y
, y  una secuencia tal que
una secuencia tal que 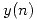 sea igual a la
sea igual a la 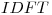 de (
de (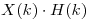 ),justificando la cantidad elegida de puntos de
),justificando la cantidad elegida de puntos de 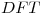 . Graficar
. Graficar  ,
,  y
y  .
.
Punto III
Sea un sistema 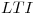 con respuesta impulsiva
con respuesta impulsiva  y respuesta en frecuencia
y respuesta en frecuencia  , del cual se tienen los siguientes datos:
, del cual se tienen los siguientes datos:
- El sistema es causal.
 .
. - La Transformada de Fourier de
 es real.
es real.
- Demostrar que el sistema es
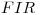 .
. - Sabiendo ademas que
 ,
, 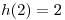 , y
, y  , encontrar
, encontrar  .
.
Resolución
Punto I
Punto II
- Para resolver este inciso se tiene en cuenta que multiplicar en frecuencia es convolucionar en tiempo. Por inspección se sabe que la antitransformada de
 va a ser una suma de deltas. La convolución de una señal con una delta es simplemente “pegar” la señal donde cae la delta.
va a ser una suma de deltas. La convolución de una señal con una delta es simplemente “pegar” la señal donde cae la delta.
Sea 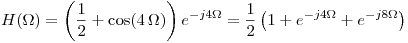
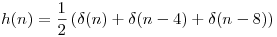
Entonces 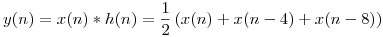
Punto III
Para demostrar que ![<tex>h[n]</tex> <tex>h[n]</tex>](lib/plugins/latex/images/abc0247dc55ce63b2042325995657b41b8fec4f6_0.png) es finita (sistema
es finita (sistema 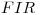 ) se analizan los puntos planteados por el problema.
) se analizan los puntos planteados por el problema.
Que el sistema sea causal significa que ![<tex>h[n]=0 \ n<0</tex> <tex>h[n]=0 \ n<0</tex>](lib/plugins/latex/images/fa609261b596174b3b241d66bf716aa985e55424_0.png) . Además
. Además ![<tex>h[n]</tex> <tex>h[n]</tex>](lib/plugins/latex/images/abc0247dc55ce63b2042325995657b41b8fec4f6_0.png) es real ya que
es real ya que  . Por ultimo, la Transformada de Fourier de
. Por ultimo, la Transformada de Fourier de ![<tex>h[n + 2]</tex> <tex>h[n + 2]</tex>](lib/plugins/latex/images/1b00a8188aa00cc7ce6a2cdf31a050d8cf051e3b_0.png) es real, entonces
es real, entonces ![<tex>h[n]</tex> <tex>h[n]</tex>](lib/plugins/latex/images/abc0247dc55ce63b2042325995657b41b8fec4f6_0.png) es par respectode dos.
es par respectode dos.
Teniendo en cuenta lo dicho anteriormente se puede decir que ![<tex>h[n] \not= 0 \Leftrightarrow 0<n<4</tex> <tex>h[n] \not= 0 \Leftrightarrow 0<n<4</tex>](lib/plugins/latex/images/2470a9ec38ced2c858127da42c5b4b0b9682c243_0.png) . Por consiguiente el sistema es
. Por consiguiente el sistema es 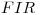 .
.
Para hallar se analizan los datos del segundo inciso:
Por definicion ![<tex>H(\Omega) = \sum_{-\infty}^{\infty} x[n] e^{-j\Omega n} </tex> <tex>H(\Omega) = \sum_{-\infty}^{\infty} x[n] e^{-j\Omega n} </tex>](lib/plugins/latex/images/bb76dc62aa1606aaddfbee13017ab461da248204_0.png) , entonces
, entonces ![<tex>H(0) = \sum_{-\infty}^{\infty} h[n] = h[0] + h[1] + h[2] + h[3] + h[4] = 10</tex> <tex>H(0) = \sum_{-\infty}^{\infty} h[n] = h[0] + h[1] + h[2] + h[3] + h[4] = 10</tex>](lib/plugins/latex/images/adc53e451f41231c52ee1c7a9ae7f123d7302a75_0.png) .
.
Por otra parte  . Antitransformando a ambos lados se tiene
. Antitransformando a ambos lados se tiene ![<tex>h[n] = (-1)^n h[n] </tex> <tex>h[n] = (-1)^n h[n] </tex>](lib/plugins/latex/images/70c22f21a1113bd2fea52d8b523a2ab6e882c058_0.png) . Luego
. Luego ![<tex> h[n] = 0 </tex> <tex> h[n] = 0 </tex>](lib/plugins/latex/images/2e2263b40cf991eed8adea9ca307c76f3b982f75_0.png) para
para 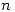 impar por ser la respuesta al impulso una función par.
impar por ser la respuesta al impulso una función par.
Con la ultima condición, ![<tex>h[2] = 2</tex> <tex>h[2] = 2</tex>](lib/plugins/latex/images/bfe30a79239cc43439171222d070392e59ac0fa3_0.png) , se puede determinar completamente la respuesta impulsiva.
, se puede determinar completamente la respuesta impulsiva.
En sintesis:
![<tex> h[n] </tex> <tex> h[n] </tex>](lib/plugins/latex/images/0a3dea7b4ee13dd08ce989ffe1392553eff4963f_0.png) es par.
es par. ![<tex> h[0] + h[2] + h[4] = 10</tex> <tex> h[0] + h[2] + h[4] = 10</tex>](lib/plugins/latex/images/69f4f4c4d75b726c31ec5b0a35915f1d8759a3b0_0.png) .
.![<tex>h[2] = 2</tex> <tex>h[2] = 2</tex>](lib/plugins/latex/images/bfe30a79239cc43439171222d070392e59ac0fa3_0.png) .
.
Entonces

