Coloquio - 66.74. Señales y Sistemas

Cátedra: Todas
Día: 30/07/2007

Una señal es la entrada de un sistema 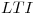estable cuya función de sistema viene dada por

Si 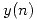es la salida de dicho sistema, se pide

1. Encontrar 0,1,2. Debe especificar los valores numéricos.
2. Se plantea como alternativa para encontrar 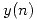en los valores pedidos, utilizar 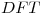, siguiendo los siguientes pasos: en primer lugar se muestrea 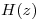sobre el círculo unitario en 3 puntos equiespaciados, y con ellos se forma el vector 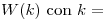0,1,2. Luego se multiplica por la 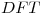de 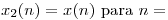0,1,2 Y 0 para otro . De dicho producto se obtiene la secuencia 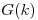. Finalmente se hace la 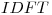de 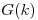obteniéndose una secuencia que denominamos 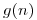. Indicar si se cumple que 0,1,2. En caso de ser cierto justifique adecuadamente por qué, y si no lo es indique un procedimiento que solamente use el algoritmo de cálculo de para obtener 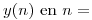0,1,2. En ese caso indique mediante un diagrama en bloques cada que utilice, indicando claramente los vectores y el tamaño de estos, así como de la cantidad de puntos de 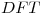usada en cada bloque.

Se definen dos sistemas. El primero, sistema 1, definido por la figura. Asuma que dicho sistema es causal, que Y que . El segundo, sistema 2, viene definido por la cascada de un sistema 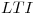causal cuya función de sistema viene dada por seguido de un bloque de sobremuestreo por un factor .

1. Encuentre la expresión analítica cerrada y mínima de la respuesta impulsiva de ambos sistemfls.
2. Determine la expresión mínima de la salida de ambos sistemas ante la entrada .
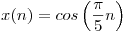3. En base a los resultados obtenidos, establezca una conclusión sobre la posible equivalencia entre ambos sistemas.

Para convertir una señal senoidal 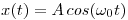en una señal constante de amplitud , se implementa el siguiente sistema discreto: la señal es muestreada con un período de muestreo obteniéndose la señal discreta 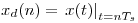se la eleva al cuadrado, y se la pasa por un filtro pasabajos cuyo espectro periódico se muestra en la figura siguiente entre y .

Si las frecuencias posibles de la señal están dentro de un rango de , determinar si existe un período de muestreo tal que toda otra componente del espectro de salida que no corresponda a la señal constante de amplitud , caiga en la zona de mayor atenuación del filtro .