Coloquio - 66.74. Señales y Sistemas

Cátedra: Todas
Día: 24/07/2007

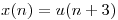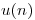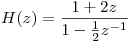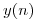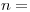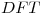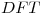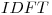Una señal donde es el escalón unitario, ingresa a un sistema a derecha cuya función de sistema es . Se desea determinar la salida para 3, 4, 5, 6, 7 usando . Se dispone de una función que calcula e . Dicha función no completa automáticamente con ceros, sino que éstos deben ser agregados al vector de entrada de ser necesario en las posiciones que correspondan. Es posible determinar en forma exacta en los puntos considerados, usando solamente dicha función (el número de veces que se desee)?. Si no es posible explique claramente porqué. Si es posible explique el procedimiento para realizarlo. En este caso deben determinarse explícitamente los valores del vector que se ingresa en la 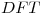cada vez que dicha función sea usada. Su explicación debe ser tal que pueda ser volcada a un programa que sin ambiguedades.

Sea un sistema LTI definido por la siguiente función de sistema:

1. Sin determinar 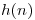explícitamente, y sin utilizar consideraciones temporales, determinar justificando si las siguientes afirmaciones son correctas o incorrectas. Si no cuenta con información suficiente determinar que información adicional requeriría para determinar la veracidad de las mismas.
   1. El sistema es estable.
   2. El sistema es causal.
   3. El sistema no tiene fase lineal.
2. Determine la expresión mas simple posible de .

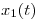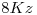Dos señales y , limitadas en banda a y respectivamente, son digitalizadas con un coversor ideal a frecuencias de 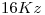y respectivamente. Partiendo de dichas señales digitalizadas que llamaremos 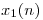y , se desea obtener . Para ello se dispone de un conversor ideal que puede ser utilizado una sola vez.

1. Indique mediante un diagrama en bloques el sistema que logra dicho objetivo, mostrando claramente la función de cada bloque.
2. Grafique indicando valores numéricos los espectros parciales que resulten de cada paso que realize.
3. Indique en la frecuencia del conversor con el que se obtiene la señal resultante.

Debe indicar los valores numéricos de los parámetros de cada bloque que utilice y los valores relevantes de los gáficos para que éste ejercicio tenga validez.