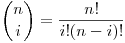ENUNCIADO [Foros-FIUBA::Wiki]

NOTA: El final fue inventado en el momento por Abate, primero dio un ejercicio de una montaña rusa muy similar al que puso despues, pero como ya habiamos hecho una montaña rusa en un TP lo cambio.

ENUNCIADO

1

Se tiene una superficie de Bezier (son las que salen de 2 curvas de Bezier) con 4 puntos de control en cada curva. Tambien se cuenta con una primitiva DibujarCasa() que dibuja una casa con centro en el origen. Se pide hacer 3 funciones en usando OpenGL (pero me parece que no es muy necesario): *ArmarCiudad ( int N, int M, puntos* pCtrl1, puntos* pCtrl2) *Display1(float x1,float y1,float x2,float y2) *Display2(float h)

ArmarCiudad tiene que poner N*M casas distribuidas uniformemente en la superficie . Los puntos de control de cada curva son los que les puse pCtrl1 y 2.

Display1 tiene que generar una vista en perspectiva con el observador en (x1,y1) mirando en la direccion (x2,y2). Se puede usar gluLookAt y glPerspective.

Display2 tiene que generar una vista ortografica desde arriba con el observador a una altura h. Se puede usar gluLookAt y glOrtho.

2 (este me toco a mi pero me parece que otros les dio uno distinto)

Demostrar que las bases de Berstein son recursivas asi: $<tex> B_i^n(t) = (1-t)*B_i^{n-1}(t) + t*B_{i-1}^{n-1}(t) </tex>$

RESOLUCION

2

Partiendo de la definicion de las bases de Berstein: 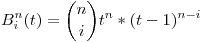$<tex> B_i^n(t) = {n \choose i} t^n*(t-1)^{n-i} </tex>$ se reemplaza en la ecuacion que pide demostrar y sale solo. Solo hay que recordar que $<tex> {n \choose i} = \frac{n!}{i! (n - i)!} </tex>$