• Ventajas y desventajas de los controladores P, PI, PD y PID

El agregado de un tiempo muerto (demora) a un sistema

1. Contribuye a su estabilidad
2. Lo puede volver inestable
3. Le produce un adelanto de fase
4. No afecta su respuesta de frecuencia en cuanto al atraso de fase

Lo puede volver inestable.

En el Ogata, 5ed. Había un dibujito de qué pasaba con el Root Locus para un caso con retardo de transporte (tiempo muerto o lag), no lo encuentro. Usando las propiedades de la transformada de Fourier, al agregar un retardo de 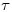, la fase de la transferecia queda: , o sea, retrasa la fase. Baja Margen de Fase ⇒ Más inestable.

Si se tiene un lazo con un PID y se produce una variación tipo rampa del error

1. La accion derivativa producirá un incremento inmediato de la salida en forma de escalón
2. La acción proporcional producirá un incremento de salida en forma de parábola
3. La acción integral producirá un incremento de salida en forma de rampa
4. Todas son correctas

Opción 1.

Un PID es de la forma: Superponiendo cada efecto, podemos decir que:

• El P producirá una salida en forma de rampa
• El I producirá una salida en forma de parábola
• El D producirá una salida en forma de escalón

Leyendo bien el enunciado, sólo es verdadera la opción 1 (las otras están al reves). Para esto, hay que considerar que la señal de mando a la salida es la superposición de los tres efectos, y a menos que el PID esté trabajando como un P, un I o un D, la salida no será ni una rampa, ni un escalón ni una parábola.

La siguiente transferencia corresponde a:

1. una acción proporcional
2. una acción derivativa aproximada
3. un filtro pasa-bajos
4. una acción integral aproximada

Opción 2.

Esa transferencia es un pasa altos, así que descartamos la 3. No es una acción proporcional porque no es proporcional :P Una acción integral es un polo en el origen. Una acción derivativa es un cero en el origen. Dado que tener una acción derivativa real implicaría un ancho de banda infinito, y cosas así, es de pensar que la transferencia deje de crecer en algún momento. El polo en -1 hace eso. En un rango de frecuencias de 0rad a 0.1rad se comportaría como un derivador (el 0.1 digo por el tema de la fase del polo, una década antes)

1. El máximo sobrepico correspondiente a la respuesta al escalón del siguiente sistema nunca será mayor al 100% si tanto como y T si todos ellos son positivos.
2. Sea la siguiente ecuación característica de un sistema lineal , al aumentar el valor de K aumentará la frecuencia de oscilación del sistema.
3. Para el sistema del punto anterior, si se aumenta el coeficiente del término en 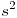, generalmente mejorará el amortiguamiento del sistema
4. Un controlador PID disminuye en uno el número de asíntotas
5. Un sistema cuya función de transferencia a lazo abierto incluye un retardo puro es, a lazo cerrado, menos estable que el correspondiente a la misma transferencia sin el retardo.
6. El controlador PD siempre disminuye el máximo sobrepico correspondiente a la respuesta al escalón del sistema a lazo cerrado

1. Falsa. ¿Por qué? –> NO SE! Para mí es verdadera.
2. Verdadera. Sale de ver el Root Locus. Ver abajo
3. Verdadera. Ver abajo.
4. Verdadera. Un PID es un polo y 2 ceros ⇒ Aumenta en 1 la cantidad de ceros ⇒ Disminuye la cant. de asíntotas en 1.
5. Verdadera. El retardo mete un retraso de fase lineal. Baja MF.
6. Falsa. Depende de cómo lo sintonizes. Un PD es cero en ⇒ Es un pasa-altos: si lo ponés a una frecuencia menor que la de la osclación la vas a amplificar.

(Ogata(en) 5ed. Ej A-6-20 p.392) Tenemos un sistema con una ecuación característica , esto sería .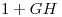

Para hacer Root Locus, necesitamos llevar el GH a la forma:

En este caso, vamos a partir de : divido todo por los términos que no tienen K:

queda entonces:

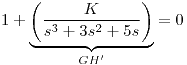
Luego, el Root Locus de mi sistema es equivalente al del sistema dado por:

Cuyo Root Locus (para K>0) es:

Ahora multiplicamos el coeficiente cuadrático por un valor

Es sencillo saber cómo se mueven los polos complejo-conjugados con lambda:

Lo cual provoca que el coeficiente de amortiguamiento suba:

Indique cuál de las siguientes afirmaciones es verdadera.

1. El Controlador PI reduce el Margen de Fase y la Frecuencia de Cruce de Ganancia.
2. El Controlador PD en todos los casos mejora el error en régimen permanente.
3. El Controlador PD reduce el Margen de Fase y la Frecuencia de Cruce de Ganancia.
4. El controlador PD siempre disminuye el máximo sobrepico correspondiente a la respuesta al escalón del sistema a lazo cerrado.

A ver…

El PI es un polo en . O sea, me tira el Bode “para abajo”, tanto en módulo como en fase. Hace que la Frecuencia de Cruce de Ganancia (cuando la transferencia es 0dB) se reduzca, y de misma forma pasa con el margen de ganancia, ya que si bien la fase aumentaría por irse la frecuencia más atras, se le restan 90º por el polo. Tiene sentido (aunque no se si esta respuesta tiene un contraejemplo que no veo).

Se definen las figuras de mérito para los errores de posición, velocidad y aceleración como:

Un controlador PD tiene una . Vemos que al agregarlo, queda:

Es decir, mejoran las figuras de mérito sólo si , no siempre.

No, por el contrario, los aumenta. Hace lo contrario que el PI: al ser un cero, “sube” el Bode de GH(s).

La verdad, no sé. Un PD pone un cero a lazo abierto ⇒ Me saca una asíntota (si la hubiese)… pero el sobrepico depente de y depende de la ganancia, que es variable… así que no necesariamente: puedo poner un PD y con el cero tiro el lugar de las raices a la izquerda, pero al mismo tiempo puedo mandar las raices a la loma del tuje tocando la . Así que digamos que es falsa.