66.02 Laboratorio - Examen Final Integrador - 22/12/2011
Cátedra: única/todos los cursos
Fecha: primera del primer cuatrimestre del 2007
Día: 22/12/2011
Enunciado
Punto I (Informática)
Clásico circuito para medir resistencia con voltímetro y amperímetro. El objetivo es medir R con una incertidumbre relativa menor a 5%. Indicar si este objetivo es alcanzable. La fuente tiene 50V.
(Circuito para medir I y V sobre un resistencia conectada a una fuente de CC. Conexión TBM)
Punto II (Informática)
Se mide una señal de intensidad de corriente periódica; un periodo de dicha señal se muestra en la figura. A) ¿Qué lectura se obtiene con MMA en modo CC? B) ¿Qué lectura se obtiene con un MMD de verdadero valor eficaz (modo CA)? Ayuda: el área debajo de la curva f(x)=x^n (n positivo) es 1/(n+1) el área del rectángulo que contiene a dicha curva.
Punto VI (Electrónica e Informática)
Considere los conceptos de ajuste, calibración y compensación; exponga similitudes y diferencias entre los mismos.
Punto VII (Informática)
Se tienen 2 amperímetro: A1 (alcance = 1mA, clase = 1, res. equiv = 100 Ohms) y A2 (alcance = 5mA, clase = 2, res. equiv = 100 Ohms). Encontrar alcance, clase y resistencia equivalente de la composición de dichos instrumentos A) en serie, B) en paralelo.
Punto VIII (Electrónica e Informática)
Observe el circuito de la figura (unidades: V, kOhm). Según Kirchhoff, la intensidad de corriente en la pila debe ser igual a la suma de las intensidades de corriente en los resistores; para comprobar la afirmación de Kirchhoff, con un único amperímetro (alcance = 100 mA, clase = 1, res. equiv = 100 Ohms, cant. divisiones = 100) se hacen tres mediciones en secuencia: a) intensidad de la pila (insertar amp. entre A y B), b) intensidad de R1 (insertar amp. entre C y D), c) intensidad de R2 (insertar amp. entre E y F); ¿tiene algún comentario sobre el experimento?; dentro de la incertidumbre obtenible en la medición, ¿confirma o desmiente la ley de Kirchhoff?
Abreviaciones
- CC: corriente contínua.
- MMD: multímetro digital.
- MMA: multímetro analógico.
- pap: pico a pico, beso a beso.
Resolución
Punto I
La cosa creo que va así:
Hay que usar los modelos de amperímetro y voltimetro “real” en el circuito (esto es, incluir las resistencias Ra y Rv) y hallar la corriente que circula por el resistor R.
Sabemos que R = V/I (1)
Como la tensión medida por el voltímetro es la que cae en la resistencia, empleamos este valor medido (con su respectiva incertidumbre). En cuanto a la corriente, no es exactamente la que acusa el amperímetro, esto es debido al efecto de carga que produce el voltímetro y de la resistencia interna del amperímetro.
De la ecuación de I_R obtenida anteriormente, empleando el método de las derivadas, obtenemos delta I_R.
Reemplazando en la ley de ohm (1), obtenemos R y delta R
Hallamos la incerteza relativa de R, er{R} = R / delta R y pedimos que sea menor o igual al valor dado en el enunciado. De aquí obtenemos el valor máximo que puede llegar a tener R para poder medir debajo de es incerteza.
Punto II
El MMA en modo CC mide el valor medio de dicha señal.
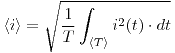
Resolviendo la integral (sale practicamente a ojo), tenemos 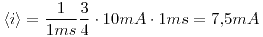 Dentro de la incerteza del instrumento, ese es el valor que debería medir.
Dentro de la incerteza del instrumento, ese es el valor que debería medir.
Para el MMD de verdadero valor eficaz (true RMS) hay que recordar que este está en modo AC y por lo tanto, no tiene en cuenta el valor de continua de la señal.
Hay dos formas equivalentes de resolverlo. Podemos quitarle la componente de continua a nuestra señal restando el valor medio previamente calculado en el ítem anterior, y a esta, calcularle el valor eficaz.
Otra opción es empleando:
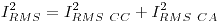 Entonces, podemos calcular el valor eficaz de la señal montada sobre continua, el de la continua por otra parte y despejar el de la señal sin componente de continua.
Entonces, podemos calcular el valor eficaz de la señal montada sobre continua, el de la continua por otra parte y despejar el de la señal sin componente de continua.
Prestando atención al emplear el 1º método, podemos llegar a la deducción de la ecuación antes presentada.
Haciendo el segúndo método tenenmos:
![<tex>I^2_{RMS} = \frac{1}{1ms} \left[\int_{0}^{0.5ms} {\left(20 \frac{mA}{ms}\right)^2 t^2 \cdot dt} + \int_{0.5ms}^{1ms} {(10 mA)^2 \cdot dt}\right] = 66.66 (mA)^2</tex> <tex>I^2_{RMS} = \frac{1}{1ms} \left[\int_{0}^{0.5ms} {\left(20 \frac{mA}{ms}\right)^2 t^2 \cdot dt} + \int_{0.5ms}^{1ms} {(10 mA)^2 \cdot dt}\right] = 66.66 (mA)^2</tex>](lib/plugins/latex/images/6c7aa443e2dd36318debae1ea3db6f9f4e0f916e_0.png)
Luego, para la componente de continua:
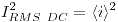 (ante la duda, resolver la integral
(ante la duda, resolver la integral ![]() )
)
Finalmente:
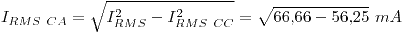
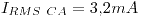
Que es el valor que, dentro de la incetidumbre de la medición, debe acusar el MMD.
Punto VI
Punto VII
Este es relativamente sencillo. Hay que recordar que la clase de un instrumento es el error relativo de la incerteza multiplicado por 100, entonces, cuando se habla de clase se está hablando de incerteza relativa.
Al poner dos amperímetros en serie, sus resistencias internas se suman. Por lo tanto, la resistencia equivalente es la suma de las de cada uno.
El alcance es el del menor instrumento; ya que ambos MMA miden la misma corriente, el maximo de corriente que podrán medir está dado por el instrumento con menor alcance. Si bien luego que el primero se vaya de escala se podría seguir midiendo con el segundo se estaría comprometiendo la integridad de los galvanómetros.
En este caso, los dos instrumento tienen alcances muy distintos, por lo cual cuando uno esté a fondo de escala el otro estará a un quinto de cero; esto hace que la medición del segundo multímetro no se relevante, y solo se tenga en cuenta la de A1. En conclusión, A2 actua como una resistencia en serie, cuyo unico desproposito es aumentar la R. eq.
Por lo dicho antes:
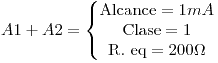
Ahora con los dos amperímetros en paralelo:
La corriente total medida por el “nuevo” instrumento es la suma del valor medido por A1 y el de A2. (*)
La resistencia equivalente es el paralelo del de A1 y A2, como se puede observar planteando el circuito equivalente.
El alcance es el máximo valor que puede circular por el “nuevo” instrumento hasta que uno de los amperímetros se valla de escala. Por la configuración dada, la corriente que entra se reparte equitativamente a cada amperímetro (ya que poseen indentica R. eq). El máximo será cuando por A1 circule 1mA; en esta situación circularán 1mA por A2, ergo, la corriente máxima (y por ende, el alcance) es de 2mA.
Lo más complicadito es la clase. Para conocerla, hallamos el \xi{I_T}.
Sabemos que:
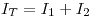 (Por lo dicho en un principio*)
(Por lo dicho en un principio*)
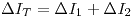
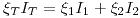
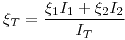
Bajo la hipótesis de que ambos instrumentos tienen la misma R. eq. podemos decir que
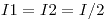
y por lo tanto, la expresión anterior se reduce a:
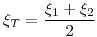
En resumen:
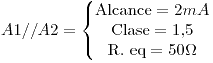
Punto V
Discusión
keyword: Creo que el punto de los amperímetros en parelelo está mal determinada la clase. El error no es clase * valor medido, es clase * alcance


