Parcial - 65.06. Máquinas Eléctricas - 21/05/2007

2007

Cátedra: Examen único tomado en conjunto por las dos cátedras
Fecha: 1º Oportunidad - 1º Cuatrimestre 2007
Día: 21/05/2007

Enunciado

P1:Transformador

Monofásico, S_N = 100 kVA, U_1N = 1000 V, X'_e = 5 %
Q de magnetización = 3 kVAr. Pérdidas: en cobre 2%, en hierro 1 %.
Carga: 100 kVA, Factor de potencia = 0,9.

Calcular:

Rendimiento η con esa carga
Corriente de vacío
Carga para rendimiento máximo
El rendimiento máximo

P2:MAT

Motor de 6 polos, línea de 3 x 380 V, 50 Hz
Impedancia por fase del circuito equivalente referido al estator:
Z₁ = 0,04 + j 0,14 Ω Z'₂ = 0,03 + j 0,125 Ω
P_Fe = 1500 W P_mec = 1200 W I_m = 7 A

Para un deslizamiento del 3% calcular:

La velocidad de giro del motor (RPM)
Potencia de salida P_S (kW)
Rendimiento η
Factor de potencia cos φ

Calcular además la corriente y la cupla de arranque (directo).

Teórico

Determinación de la curva de cupla en función del deslizamiento para un MAT.

Laboratorio

Ensayo directo de MAT realizado en el laboratorio.

Circuito del ensayo
Descripción del freno y su funcionamiento
Explicar cómo se arranca el motor
Describir cómo se determina la potencia mecánica entregada por el motor
Ídem para la potencia eléctrica absorbida

El estado de carga C es 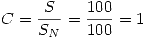$<tex>C = \frac{S}{{S_N }} = \frac{{100}}{{100}} = 1</tex>$ .
La potencia de pérdida de corto circuito es P_CCo = 2 % = 0,02 . S_N = 0,02 . 100 kVA = 2 kW.
La potencia de pérdida en el hierro es P_Fe = 1 % = 0,01 . S_N = 0,01 . 100 kVA = 1 kW.

Según la fórmula de rendimiento para transformador monofásico: 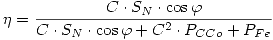$<tex>\eta = \frac{{C \cdot S_N \cdot \cos \varphi }}{{C \cdot S_N \cdot \cos \varphi + C^2 \cdot P_{CCo} + P_{Fe} }}</tex>$ . Reemplazando los valores resulta η = 96,7 %.

2) Corriente de vacío

Se considerando el circuito simplificado del transformador en el que se coloca la rama paralelo a la entrada y luego la impedancia equivalente. Cuando se conecta este circuito en vacío, no circula corriente por la impedancia equivalente y la corriente sólo circula por la rama paralelo.
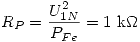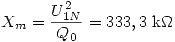Así, en vacío se puede plantear que: $<tex>R_P = \frac{{U_{1N}^2 }}{{P_{Fe} }} = 1\mbox{ k}\Omega</tex>$ y que $<tex>X_m = \frac{{U_{1N}^2 }}{{Q_0 }} = 333,3\mbox{ k}\Omega</tex>$ , con lo que resulta 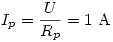$<tex>I_p = \frac{U}{{R_p }} = 1\mbox{ A}</tex>$ e $<tex>I_m = \frac{U}{{X_m }} = 3\mbox{ A}</tex>$ .
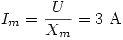Como estas corrientes se encuentran en cuadratura, 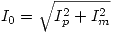$<tex>I_0 = \sqrt {I_p^2 + I_m^2 } </tex>$ y resulta I₀ = 3,16 A.

3) Carga para rendimiento máximo

Se puede demostrar que 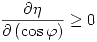$<tex>\frac{{\partial \eta }}{{\partial \left( {\cos \varphi } \right)}} \geq 0</tex>$ , por lo que el máximo rendimiento se dará por un lado con un FP = 1. Por otro lado, se demuestra que 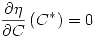$<tex>\frac{{\partial \eta }}{{\partial C}}\left( {C^* } \right) = 0</tex>$ y resulta un máximo para 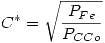$<tex>C^* = \sqrt {\frac{{P_{Fe} }}{{P_{CCo} }}}</tex>$ , que es el estado de carga para el cual se igualan las potencias de pérdida en el cobre y en el hierro. Resulta C* = 0,707.
Entonces, S* = C* . S_N = 70,7 kVA. Por lo tanto, la carga para rendimiento máximo es una carga de P = 70,7 kW y puramente resistiva (FP = 1).

4) El rendimiento máximo

Utilizando la fórmula de rendimiento del punto 1 pero con C* = 0,707 y cos $<tex>\varphi</tex>$ = 1, resulta η = 97,2 %.

P2:MAT

La velocidad de giro resulta: 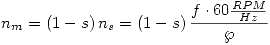$<tex>n_m = \left( {1 - s} \right)n_s = \left( {1 - s} \right)\frac{{f \cdot 60{\textstyle{{RPM} \over {Hz}}}}}{\wp }</tex>$ , siendo la cantidad de pares de polos del motor.
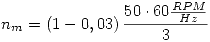$<tex>n_m = \left( {1 - 0,03} \right)\frac{{50 \cdot 60{\textstyle{{RPM} \over {Hz}}}}}{3}</tex>$ → n_m = 970 RPM.

Se considera el siguiente circuito equivalente:

Las pérdidas en el hierro serán tenidas en cuenta en forma adicional al circuito.

No indica el tipo de conexión del motor. Después de consultar al ayudante, aclaró de considerarlo conectado en estrella.

Falta determinar X_m. Para esto se usan los datos de vacío. En vacío, 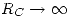$<tex>R_C \to \infty </tex>$ , por lo que la corriente circula sólo por Z₁ y por la inductancia X_m.
Entonces resulta: 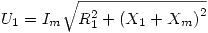$<tex>U_1 = I_m \sqrt {R_1^2 + \left( {X_1 + X_m } \right)^2 } </tex>$ . Despejando, X_m = 31,29 Ω.
Planteando el circuito equivalente de Thèvenin, resulta:

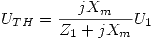$<tex>U_{TH} = \frac{{jX_m }}{{Z_1 + jX_m }}U_1 </tex>$ . Considerando U₁ con fase 0, entonces: U_TH = 219,02 ∠ 0,07292º.
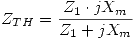$<tex>Z_{TH} = \frac{{Z_1 \cdot jX_m }}{{Z_1 + jX_m }}</tex>$ → Z_TH = 0,14495 ∠ 74,12º.
Se puede calcular 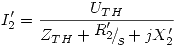$<tex>I'_2 = \frac{{U_{TH} }}{{Z_{TH} + {\raise0.7ex\hbox{${R'_2 }$} \!\mathord{\left/ {\vphantom {{R'_2 } s}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$s$}} + jX'_2 }}</tex>$ → I’₂ = 204,17 ∠ –14,197º.
Por lo tanto, 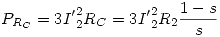$<tex>P_{R_C } = 3{I'}_2^2 R_C = 3{I'}_2^2 R_2 \frac{{1 - s}}{s}</tex>$ → P_Rc = 121,3 kW
La potencia de salida resulta: P_S = P_Rc – P_mec – P_Fe → P_S= 118,6 kW

Recordar agregar la P_Fe que no es tenida en cuenta en el circuito.

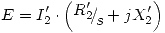$<tex>E = I'_2 \cdot \left( {{\raise0.7ex\hbox{${R'_2 }$} \!\mathord{\left/ {\vphantom {{R'_2 } s}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$s$}} + jX'_2 } \right)</tex>$ = 205,76 ∠ –7,072º
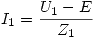$<tex>I_1 = \frac{{U_1 - E}}{{Z_1 }}</tex>$ → I₁ = 205,09 ∠ –16,02º.
P_E = P_In + P_Fe = 3 . Re(U₁ . I₁*) + P_Fe = 126,55 kW

Recordar agregar la P_Fe que no es tenida en cuenta en el circuito.

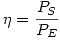$<tex>\eta = \frac{{P_S }}{{P_E }}</tex>$ → η = 93,7 %
FP = cos φ = cos [0º – (–14,197º)] → FP = 0,969

En el arranque, s = 1 y RC = 0.
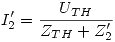$<tex>I'_2 = \frac{{U_{TH} }}{{Z_{TH} + Z'_2 }}</tex>$ → I’₂ = 800,97 ∠ –75,17º.
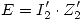$<tex>E = I'_2 \cdot Z'_2 </tex>$ = 102,96 ∠ 1,33º
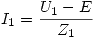$<tex>I_1 = \frac{{U_1 - E}}{{Z_1 }}</tex>$ → I₁ = 804,17 ∠ –75,22º.
∴ I_arr = 804 A

Despreciando la PFe, 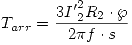$<tex>T_{arr} = \frac{{3{I'}_2^2 R_2 \cdot \wp }}{{2\pi f \cdot s}}</tex>$ → T_arr = 555,78 Nm

— 4wd 2007/05/29 02:31

Discusión

Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.