Examen Final - 64.01. Estabilidad I A - 31 de Julio de 2008
Cátedra: indistinta
Fecha: 3° Oportunidad - Invierno 2008
Día: 31/07/2008
Enunciado
Punto Práctico
Para la figura dada, se pide:
- Encontrar los momentos principales de inercia baricéntricos.
- Trazar la circunferencia de Mohr para el baricentro.
- Explicar cuáles son los ejes principales de inercia baricéntricos.
Nota: Se sugiere observar bien la figura antes de empezar a calcular cualquier cosa.
Aclaración: Los ángulos son todos iguales a 60°.
Tiempo asignado a este ejercicio: 30 min, máximo 45 min. Es corregido en el momento por Fioravanti: el que lo tiene bien puede seguir con la parte teórica; el que no, vuelve el jueves siguiente.
La hoja del examen se entrega a cambio de la libreta firmada (o sea, con autorización para rendir coloquio), sin excepción.
Además de la figura propiamente dicha, se provee al alumno de las tablas de Área, Baricentro, Momentos de segundo orden baricéntricos y Momentos de segundo orden para las siguientes figuras:
- Círculo.
- Semicírculo.
- Cuarto de círculo.
- Sector circular de amplitud
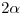 .
.
Punto Teórico
- Reticulados:
- Hipótesis básicas del modelo
- Métodos de análisis.
- Método de resolución matricial.
- Ecuaciones diferenciales para barras de eje curvo.
A mí en el examen no me pareció que fuera así (para mí es poco claro el enunciado), pero con “métodos de análisis” se refiere a los distintos métodos de resolución.
El examen teórico fue oral, a pesar de que había habido muchos inscriptos esa fecha (lo que pasó es que ya con el práctico había volado la mitad (o más) de los inscriptos).
Las consignas están escritas en el pizarrón, y una vez que Fioravanti te dice que aprobaste el práctico, te ponés a desarrollar los temas por escrito. Cada tanto los profesores preguntan si alguien ya terminó, y se disponen a tomarle el oral.
Resolución
Punto Práctico
1
Los momentos pedidos,  y
y 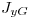 , surgen de considerar la siguiente subfigura 1:
, surgen de considerar la siguiente subfigura 1:
cuyos momentos  y
y  respecto de los ejes
respecto de los ejes  e
e  1) dibujados salen de la tabla adjunta, y valen:
1) dibujados salen de la tabla adjunta, y valen:
 .
.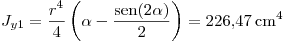 .
.
Ojo que  , pues según la tabla es la mitad de la amplitud del sector circular.
, pues según la tabla es la mitad de la amplitud del sector circular.
Seguidamente, consideramos la subfigura 2:
cuyos momentos  y
y  respecto de los ejes
respecto de los ejes  e
e  2) dibujados salen de la tabla adjunta, y valen:
2) dibujados salen de la tabla adjunta, y valen:
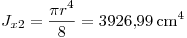 .
.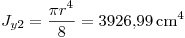 .
.
Finalmente, los momentos pedidos se encuentran sumando los de la subfigura 1 a los de la subfigura 2, y luego restando al resultado los de la subfigura 1, puesto que no queremos un semicírculo más un sector circular, sino que al semicírculo le debemos restar otro sector circular igual al primero, para así obtener aquel símbolo radiactivo:
 .
. .
.
2
Este punto es en extremo sencillo, pues como los ejes  e
e  son baricéntricos y principales de inercia, el polo
son baricéntricos y principales de inercia, el polo  de la circunferencia de Mohr coincide con su centro
de la circunferencia de Mohr coincide con su centro  , pues
, pues 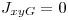 y
y  . Con lo cual:
. Con lo cual:
3
Los ejes  e
e  son ejes principales de inercia baricéntricos pues:
son ejes principales de inercia baricéntricos pues:
- Son conjugados de inercia:
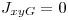 pues, por razones de simetría, el
pues, por razones de simetría, el  del sector 1 que está en el cuarto de plano
del sector 1 que está en el cuarto de plano  se compensa con el
se compensa con el  del 2 que está en el plano
del 2 que está en el plano  , y similarmente el
, y similarmente el  del sector 3 que está en el semiplano
del sector 3 que está en el semiplano 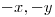 se compensa con el
se compensa con el  del 4 que está en el semiplano
del 4 que está en el semiplano  .
. - Son perpendiculares.
- El baricentro se encuentra en
 por razones de simetría.
por razones de simetría.
Punto Teórico
1
- Hipótesis básicas del modelo:
- Barras de eje recto.
- Articulaciones en los extremos.
- Cargas concentradas en los apoyos.
- Métodos de análisis:
- Por nodos.
- Por Ritter/secciones.
- Por trabajos virtuales.
- Método de resolución matricial:
Aclaración: esta resolución es para reticulados planos. Se puede ampliar fácilmente al espacio tridimensional, pero no tengo ganas de desarrollarlo. Además, si lo planteás para el plano está bien, no creo que te lo pidan para reticulados en 3D.
Para cada nodo se plantean 2 (dos) ecuaciones de equilibrio3), en las cuales intervienen (en general):
- Reacciones de Vínculo (si hubiera).
- Fuerzas externas (si las hubiera).
- Fuerzas de las barras (producto del esfuerzo interno axil).
Por otro lado, dependiendo de la disposición de los ejes (que, por comodidad, se elige una sola vez y se mantiene para todos los nodos considerados), en el caso más general cada una de estas fuerzas estará multiplicada por un  o por un
o por un  (donde
(donde  es el argumento de la fuerza considerada).
es el argumento de la fuerza considerada).
Luego de plantear las  ecuaciones4), podemos plantear una matriz
ecuaciones4), podemos plantear una matriz  de esta pinta:
de esta pinta:
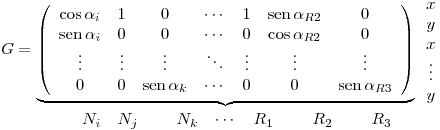
donde las filas corresponden a las ecuaciones de proyección sobre los ejes  e
e  de cada nodo
de cada nodo  ,5) y las columnas corresponden a los esfuerzos en las barras
,5) y las columnas corresponden a los esfuerzos en las barras  6) y a las reacciones de vínculo
6) y a las reacciones de vínculo 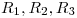 .
.
La cantidad de filas de  es
es  , y la de columnas es la cantidad de barras
, y la de columnas es la cantidad de barras  más la cantidad de reacciones de vínculo externo
más la cantidad de reacciones de vínculo externo  . La condición necesaria para que un reticulado plano sea isostático es que
. La condición necesaria para que un reticulado plano sea isostático es que  , con lo cual
, con lo cual  termina teniendo
termina teniendo  columnas:
columnas:  .
.
Ahora, consideramos un vector incógnita, que con toda originalidad llamamos  , y que contiene sólo esto:
, y que contiene sólo esto: 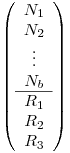 , que son justamente las incógnitas de nuestro problema. El número de filas de
, que son justamente las incógnitas de nuestro problema. El número de filas de  es igual a la cantidad de barras
es igual a la cantidad de barras  más la cantidad de reacciones de vínculo externo
más la cantidad de reacciones de vínculo externo  . La condición necesaria para que un reticulado plano sea isostático es que
. La condición necesaria para que un reticulado plano sea isostático es que  , con lo cual
, con lo cual  termina teniendo
termina teniendo  filas:
filas:  .
.
Por último, tenemos un vector  con las cargas exteriores multiplicadas por los senos y cosenos correspondientes, para cada ecuación de nodo:
con las cargas exteriores multiplicadas por los senos y cosenos correspondientes, para cada ecuación de nodo: 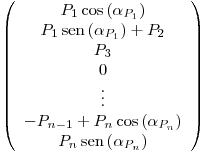 .
.  pues hay tantas filas como ecuaciones planteadas (
pues hay tantas filas como ecuaciones planteadas ( ).
).
Finalmente nos queda:

Vemos que 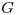 es siempre cuadrada, pero ¿es inversible? Lo será si todas sus filas son linealmente independientes, es decir, si las
es siempre cuadrada, pero ¿es inversible? Lo será si todas sus filas son linealmente independientes, es decir, si las  ecuaciones planteadas lo son. Y ello ocurrirá, precisamente, cuando además de cumplirse la condición necesaria
ecuaciones planteadas lo son. Y ello ocurrirá, precisamente, cuando además de cumplirse la condición necesaria 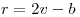 , se cumpla la condición suficiente para la isostaticidad de reticulados planos: que no exista vinculación aparente. Vemos pues que, si la matriz
, se cumpla la condición suficiente para la isostaticidad de reticulados planos: que no exista vinculación aparente. Vemos pues que, si la matriz 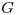 es inversible, la estructura es isostática7) y podemos plantear
es inversible, la estructura es isostática7) y podemos plantear  .
.
Discusión
 e
e  son ejes baricéntricos de la figura entera, no de estas subfiguras parciales que estamos considerando.
son ejes baricéntricos de la figura entera, no de estas subfiguras parciales que estamos considerando. es el número de nodos o vértices de la estructura reticulada que nos ocupa.
es el número de nodos o vértices de la estructura reticulada que nos ocupa. es el número de barras.
es el número de barras.





 es el número de nodos,
es el número de nodos,