Examen Parcial - 63.15. Química Analítica Instrumental - 11-05-09
Cátedra: Única
Fecha: Primera Oportunidad - Primer Cuatrimestre 2009
Día: 11/05/2009
Enunciado
Punto I
Se obtuvieron los datos siguientes cuando una muestra conocida que contiene 21.68% de hierro se analizó por un nuevo método:
| Muestra | Fe(%) |
|---|---|
| 1 | 21.64 |
| 2 | 21.80 |
| 3 | 21.77 |
| 4 | 21.40 |
| 5 | 21.74 |
- Aplique el test de Q para el resultado sospechoso y determine la posibilidad de retenerlo en este conjunto de datos para un nivel de confianza del 90%.
- Calcule la media y la desviación estándar de los porcentajes de Fe en estos datos.
Punto 2
Una serie de soluciones puede contener  ,
,  o
o  , solos o en una mezcla compatible de estas sustancias. Se dan a continuación los volúmenes de
, solos o en una mezcla compatible de estas sustancias. Se dan a continuación los volúmenes de  0.120M necesarios para titular alícuotas de 20.00mL de cada solución hasta el punto final con Verde de Bromocresol (
0.120M necesarios para titular alícuotas de 20.00mL de cada solución hasta el punto final con Verde de Bromocresol ( ) y a continuación hasta el punto final con Timolftaleína (
) y a continuación hasta el punto final con Timolftaleína ( ).
).
- Utilice esta información para determinar la composición de cada solución justificando su elección.
- Calcule la composición de las muestras (b) y © expresada en Molaridad.
| Muestra |  (mL) (mL) |  (mL) (mL) |
|---|---|---|
| (a) | 13.35 | 0.00 |
| (b) | 29.85 | 16.60 |
| © | 15.85 | 45.85 |
| (d) | 24.70 | 24.70 |
Datos:

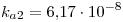
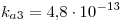
- Intervalos de pH de viraje
- Timolftaleína: 9.3-10.5
- Verde de Bromocresol: 3.8-5.4
Punto 3
Describa y explñique la respuesta de los electrodos indicadores metálicos y de membrana.
Punto 4
Obtenga la curva de conductancia versus el volumen de reactivo titulante para los siguientes agregados: 0.00mL, 4.00mL, 10.00mL, 14.00mL y 18.00mL en una titulación de 100.00mL de solución de acetato de sodio 0.0100M con ácido clorhídrico 0.100M.
Datos:
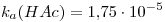
 (constante de la celda)
(constante de la celda)![<tex>\lambda^{\infty}[\Omega^{-1}cm^2eq^{-1}]</tex> <tex>\lambda^{\infty}[\Omega^{-1}cm^2eq^{-1}]</tex>](lib/plugins/latex/images/a8a2f18c3bc74c76c436ee282ce116f656adc350_0.png) :
: 
Punto 5
Exprese y represente gráficamente la ecuación de Van Deemter, indicando qué información proporciona. Explique qué fenómeno física representa cada uno de sus términos y con qué propiedades (de columna o analito) se relaciona cada uno.
Resolución
Punto I
a)Resultados ordenados: 21.40, 21.64, 21.74, 21.77, 21.80.
El más alejado es 21.40, entonces se calcula el Q como:

Se debe comparar con el valor de tablas: 
Como  el valor 21.40 no puede descartarse, ya que puede deberse a errores aleatorios con un nivel de confianza de 90%.
el valor 21.40 no puede descartarse, ya que puede deberse a errores aleatorios con un nivel de confianza de 90%.
b) Se calculó la siguiente tabla:

Entonces 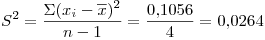

Punto 2
Parte 1
(a) Debido a que  , no hubo un segundo punto de equivalencia, es decir que la imolftaleina ha virado sin agregar
, no hubo un segundo punto de equivalencia, es decir que la imolftaleina ha virado sin agregar  , es decir que estamos en presencia de
, es decir que estamos en presencia de  solamente.
solamente.
(b) Dado que se requiere mayor cantidad de V que de T, eso indica la presencia de  y de
y de  que se neutralizan primero, y luego el
que se neutralizan primero, y luego el  pasa a
pasa a 
© Como se requiere más T que V, significa que primero se titula una especie y después dos. Por lo que la mezcla es  con
con  .
.
(d) Como  , entonces la misma especia se va neutralizando, por lo que la solución será de
, entonces la misma especia se va neutralizando, por lo que la solución será de  solamente.
solamente.
Parte 2
(b) La primera titulación:


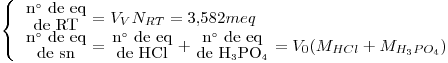

La segunda titulación: 


Por lo tanto:

© La primera titulación: 

La segunda titulación: 


Se usa 3 cifras como el dato de mayor incerteza relativa que es  con
con  de IR.
de IR.
Por lo tanto:

Punto 3
Del apunte teórico de Potenciometría:
Punto 4
La fórmula es 
Se tienen las reacciones:


![<tex>K=\frac{1}{k_a}=\frac{[\mbox{HAC}]}{[\mbox{H}^+][\mbox{Ac}^-]}</tex> <tex>K=\frac{1}{k_a}=\frac{[\mbox{HAC}]}{[\mbox{H}^+][\mbox{Ac}^-]}</tex>](lib/plugins/latex/images/28b1ada1a954652d16a3cc0c8dec8e9ee1ba4f23_0.png)
Balances de masa:
![<tex>[\mbox{Na}^+]=\frac{c_0V_0}{V_0+V}</tex> <tex>[\mbox{Na}^+]=\frac{c_0V_0}{V_0+V}</tex>](lib/plugins/latex/images/a8c75e5939b7cab249ceafbbc7a651b2a7f77028_0.png)
![<tex>[\mbox{Cl}^-]=\frac{cV}{V_0+V}</tex> <tex>[\mbox{Cl}^-]=\frac{cV}{V_0+V}</tex>](lib/plugins/latex/images/77f3ac42b047dd4105596c70815daf13149f68ca_0.png)
![<tex>[\mbox{Ac}^-]+[\mbox{HAc}]=\frac{c_0V_0}{V_0+V}</tex> <tex>[\mbox{Ac}^-]+[\mbox{HAc}]=\frac{c_0V_0}{V_0+V}</tex>](lib/plugins/latex/images/83c9ba1ccdd7ec3d7bd1983bb76410f208ba8033_0.png)
Balances de carga:
![<tex>[\mbox{H}^+]+[\mbox{Na}^+]=[\mbox{Cl}^-]+[\mbox{Ac}^-]+[\mbox{OH}^-]</tex> <tex>[\mbox{H}^+]+[\mbox{Na}^+]=[\mbox{Cl}^-]+[\mbox{Ac}^-]+[\mbox{OH}^-]</tex>](lib/plugins/latex/images/b88eeffa631c424d565d27296be9df9449049774_0.png)
Condición de equivalencia:

No hay Hcl entonces hay  en equilibrio:
en equilibrio:
![<tex>\mbox{BM}: \left\{ \begin{array}{l} \ce{[Na+]}=c_0=0.0100M \\\ce{[Ac-]} + \ce{[Ac-]} =c_0 \end{array}\right.</tex> <tex>\mbox{BM}: \left\{ \begin{array}{l} \ce{[Na+]}=c_0=0.0100M \\\ce{[Ac-]} + \ce{[Ac-]} =c_0 \end{array}\right.</tex>](lib/plugins/latex/images/db4d8e58c09865947abe122d27c0f6b312e5e9d2_0.png)
![<tex>\mbox{BC}: c_0=[\mbox{OH}^-]+[\mbox{Ac}^-]</tex> <tex>\mbox{BC}: c_0=[\mbox{OH}^-]+[\mbox{Ac}^-]</tex>](lib/plugins/latex/images/41a5a01a2dd83bb0519b9ca1bc254b1eae1a66e6_0.png) (desestimo
(desestimo  por ser medio básico)
por ser medio básico)

![<tex>K_b=\frac{K_W}{K_a}=\frac{[\mbox{OH}^-][\mbox{HAc}]}{[\mbox{Ac}^-]}</tex> <tex>K_b=\frac{K_W}{K_a}=\frac{[\mbox{OH}^-][\mbox{HAc}]}{[\mbox{Ac}^-]}</tex>](lib/plugins/latex/images/539e40c3b9fe98fe463ceadae3b33f2277bd4740_0.png)
 muy bajo, y puedo despreciar
muy bajo, y puedo despreciar ![<tex>[\mbox{OH}^-]</tex> <tex>[\mbox{OH}^-]</tex>](lib/plugins/latex/images/f534cac182c0cf0f8b09b950a825f7e14d86c133_0.png) frente a
frente a ![<tex>[\mbox{Ac}^-]</tex> <tex>[\mbox{Ac}^-]</tex>](lib/plugins/latex/images/bb5517579c1f788d402388b70816f82a8ca72e0a_0.png) en el BC, entonces:
en el BC, entonces:
![<tex>[\mbox{Ac}^-]=c_0=0.0100M</tex> <tex>[\mbox{Ac}^-]=c_0=0.0100M</tex>](lib/plugins/latex/images/311397922c1186e02c791a24764c3b16ed20cca6_0.png)

Estamos antes del PE, y el medio es básico, por lo que desesntimo  en el BC.
en el BC.
![<tex>\mbox{BM}: \left\{ \begin{array}{l} \ce{[Na+]}=9.6154\cdot 10^{-3}M \\\ce{[Cl-]}=3.8462\cdot 10^{-3}M \\\ce{[Ac-]} + \ce{[HAc]} =9.6154\cdot 10^{-3}M \end{array}\right.</tex> <tex>\mbox{BM}: \left\{ \begin{array}{l} \ce{[Na+]}=9.6154\cdot 10^{-3}M \\\ce{[Cl-]}=3.8462\cdot 10^{-3}M \\\ce{[Ac-]} + \ce{[HAc]} =9.6154\cdot 10^{-3}M \end{array}\right.</tex>](lib/plugins/latex/images/a1c35b5e3d5dd78976620928b1b117395c0153db_0.png)
![<tex>\mbox{BC}: [\mbox{Na}^+]=[\mbox{OH}^-]+[\mbox{Ac}^-]+[\mbox{Cl}^-]</tex> <tex>\mbox{BC}: [\mbox{Na}^+]=[\mbox{OH}^-]+[\mbox{Ac}^-]+[\mbox{Cl}^-]</tex>](lib/plugins/latex/images/87e66a94796cf4d9d07a01b65ebc8dd0a7af50f9_0.png)
Como todavia estamos lejos del punto de equivalencia, supondré que ![<tex>[\mbox{OH}^-]</tex> <tex>[\mbox{OH}^-]</tex>](lib/plugins/latex/images/f534cac182c0cf0f8b09b950a825f7e14d86c133_0.png) es desestimable frente a
es desestimable frente a ![<tex>[\mbox{Ac}^-]</tex> <tex>[\mbox{Ac}^-]</tex>](lib/plugins/latex/images/bb5517579c1f788d402388b70816f82a8ca72e0a_0.png) .
.
![<tex>[\mbox{Na}^+]=[\mbox{Ac}^-]+[\mbox{Cl}^-]</tex> <tex>[\mbox{Na}^+]=[\mbox{Ac}^-]+[\mbox{Cl}^-]</tex>](lib/plugins/latex/images/83385823e6900b0d9f26b2fe4171aaf2732da468_0.png)
![<tex>\frac{c_0V_0}{V_0+V}=[\mbox{Ac}^-]+f\cdot\frac{c_0V_0}{V_0+V}</tex> <tex>\frac{c_0V_0}{V_0+V}=[\mbox{Ac}^-]+f\cdot\frac{c_0V_0}{V_0+V}</tex>](lib/plugins/latex/images/0ea27be03ee67ee7f3e3ecb303dac64d804b7cdd_0.png) , donde
, donde 
![<tex>[\mbox{Ac}^-]=(1-f)\frac{c_0V_0}{V_0+V}</tex> <tex>[\mbox{Ac}^-]=(1-f)\frac{c_0V_0}{V_0+V}</tex>](lib/plugins/latex/images/a121fabc593ee0c6cbaec192c52e8c3a0262e827_0.png)
Del NM: ![<tex>[\mbox{Ac}^-] + [\mbox{HAc}]=\frac{c_0V_0}{V_0+V} \Longrightarrow [\mbox{HAc}]=f\cdot\frac{c_0V_0}{V_0+V}</tex> <tex>[\mbox{Ac}^-] + [\mbox{HAc}]=\frac{c_0V_0}{V_0+V} \Longrightarrow [\mbox{HAc}]=f\cdot\frac{c_0V_0}{V_0+V}</tex>](lib/plugins/latex/images/d96a0903cdabfd37b7f926cb3436e64f65a835d6_0.png)
![<tex>L=\frac{1}{1000 K_C} \left( \frac{c_0V_0}{V_0+V} \right) \left[ \lambda_{Ac^-}(1-f)+\lambda_{Na^+}+\lambda_{Cl^-}f \right]</tex> <tex>L=\frac{1}{1000 K_C} \left( \frac{c_0V_0}{V_0+V} \right) \left[ \lambda_{Ac^-}(1-f)+\lambda_{Na^+}+\lambda_{Cl^-}f \right]</tex>](lib/plugins/latex/images/bf72f2ec05d0561d1b09bd712eab6acc47b298b0_0.png)
Para V=4 se tiene f=0.4, por lo que  .
.
Siguen valiendo las mismas aproximaciones que el caso anterior porque estamos antes del PE, entonces la misma fórmula con f=0.8 entonces:  .
.
Es el punto de equivalencia.
![<tex>[\mbox{Na}^+]=9.091\cdot 10^{-3}M</tex> <tex>[\mbox{Na}^+]=9.091\cdot 10^{-3}M</tex>](lib/plugins/latex/images/a3ae9e2d79792297768c6e66e058b1546601302c_0.png) ,
, ![<tex>[\mbox{Cl}^-]=9.091\cdot 10^{-3}M</tex> <tex>[\mbox{Cl}^-]=9.091\cdot 10^{-3}M</tex>](lib/plugins/latex/images/33f5b71d064339a7054416581e38ff4a4f9832d8_0.png)
Todo el  puede suponerse desplazado a
puede suponerse desplazado a 
![<tex>[\mbox{HAc}]=9.091\cdot 10^{-3}M</tex> <tex>[\mbox{HAc}]=9.091\cdot 10^{-3}M</tex>](lib/plugins/latex/images/51cbacf40375167666ed56cdf20aa25a6ad55480_0.png)
Si planteo el BC desestimando ![<tex>[\mbox{OH}^-]</tex> <tex>[\mbox{OH}^-]</tex>](lib/plugins/latex/images/f534cac182c0cf0f8b09b950a825f7e14d86c133_0.png) frente a
frente a ![<tex>[\mbox{H}^+]</tex> <tex>[\mbox{H}^+]</tex>](lib/plugins/latex/images/30a82a286287b6ba18babe08a706f5aae82a5343_0.png) por ser medio ácido, entonces
por ser medio ácido, entonces
![<tex>[\mbox{Na}^+]+[\mbox{H}^+]=[\mbox{Ac}^-]+[\mbox{Cl}^-]</tex> <tex>[\mbox{Na}^+]+[\mbox{H}^+]=[\mbox{Ac}^-]+[\mbox{Cl}^-]</tex>](lib/plugins/latex/images/318e8c038053d0bb2c11a6f7bbf492d3d587f096_0.png)
![<tex>\Longrightarrow [\mbox{H}^+]=[\mbox{Ac}^-]</tex> <tex>\Longrightarrow [\mbox{H}^+]=[\mbox{Ac}^-]</tex>](lib/plugins/latex/images/74bb986d0637f6b0a9df80394353ae7fd8ce2237_0.png)
![<tex>\Longrightarrow K_a=\frac{[\mbox{H}^+][\mbox{Ac}^-]}{[\mbox{HAC}]}=\frac{[\mbox{H}^+]^2}{[\mbox{HAC}]} \Longrightarrow [\mbox{H}^+]=3.9886\cdot 10^{-4}M</tex> <tex>\Longrightarrow K_a=\frac{[\mbox{H}^+][\mbox{Ac}^-]}{[\mbox{HAC}]}=\frac{[\mbox{H}^+]^2}{[\mbox{HAC}]} \Longrightarrow [\mbox{H}^+]=3.9886\cdot 10^{-4}M</tex>](lib/plugins/latex/images/4b9787b2dbce01c050d8011d02b63c8a128f46bd_0.png) .
.
![<tex>L=\frac{1}{1000K_C} ( \lambda_{Na^+} [\mbox{Na}^+] + \lambda_{Ac^-} [\mbox{Ac}^-] + \lambda_{H^+} [\mbox{H}^+] + \lambda_{Cl^-} [\mbox{Cl}^-] ) =1.16\cdot 10^{-3}\Omega^{-1}</tex> <tex>L=\frac{1}{1000K_C} ( \lambda_{Na^+} [\mbox{Na}^+] + \lambda_{Ac^-} [\mbox{Ac}^-] + \lambda_{H^+} [\mbox{H}^+] + \lambda_{Cl^-} [\mbox{Cl}^-] ) =1.16\cdot 10^{-3}\Omega^{-1}</tex>](lib/plugins/latex/images/d5763a7a38c2bc77bcfe6af5a9151e412d451be3_0.png)
El medio ya es muy ácido, entonces el  estça en forma de
estça en forma de  , y esto lo pongo en el BM y el BC
, y esto lo pongo en el BM y el BC
![<tex>\mbox{BM}: \left\{ \begin{array}{l} \ce{[Na+]}=\frac{c_0V_0}{V_0+V} \\\ce{[Cl-]}=f \cdot \frac{c_0V_0}{V_0+V} \\\ce{[HAc]}=\frac{c_0V_0}{V_0+V} \end{array}\right.</tex> <tex>\mbox{BM}: \left\{ \begin{array}{l} \ce{[Na+]}=\frac{c_0V_0}{V_0+V} \\\ce{[Cl-]}=f \cdot \frac{c_0V_0}{V_0+V} \\\ce{[HAc]}=\frac{c_0V_0}{V_0+V} \end{array}\right.</tex>](lib/plugins/latex/images/05924e10ce591135ab846a1bc4266f96f9b9c66e_0.png)
![<tex>\mbox{BC}: [\mbox{Na}^+]+[\mbox{H}^+]=[\mbox{Cl}^-]</tex> <tex>\mbox{BC}: [\mbox{Na}^+]+[\mbox{H}^+]=[\mbox{Cl}^-]</tex>](lib/plugins/latex/images/ce56020f2ab6e648dd34d6fac8ee7a0ee673d7cf_0.png)
![<tex>\Longrightarrow [\mbox{H}^+]=(f-1)\frac{c_0V_0}{V_0+V}</tex> <tex>\Longrightarrow [\mbox{H}^+]=(f-1)\frac{c_0V_0}{V_0+V}</tex>](lib/plugins/latex/images/ba9ec21fc2987474744579025fccf762faebd568_0.png)
![<tex>L=\frac{1}{1000 K_C} \left( \frac{c_0V_0}{V_0+V} \right) \left[ \lambda_{Na^+}+\lambda_{Cl^-}f+\lambda_{H^+}(f-1) \right]</tex> <tex>L=\frac{1}{1000 K_C} \left( \frac{c_0V_0}{V_0+V} \right) \left[ \lambda_{Na^+}+\lambda_{Cl^-}f+\lambda_{H^+}(f-1) \right]</tex>](lib/plugins/latex/images/bb1778ae2e56f188cd3c0aa54d4a9d7cef1e6849_0.png)
Para este caso f=1.4, entonces 
Con las mismas suposiciones, f=1.8 entonces 
Resultados:
 |  |
|---|---|
| 0 |  |
| 4 |  |
| 8 |  |
| 10 |  |
| 14 |  |
| 18 |  |
El gráfico es:
Se graficó  vs
vs 
Punto 5
Teórico, del apunte de Cromatografía (diapositiva 13 y 14):