Fórmulas para Química Física 1 [63.06]
Termodinámica
El trabajo de compresión realizado sobre un sistema se define 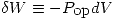
Un proceso es reversible cuando 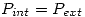 en todo el proceso.
en todo el proceso.
El Primer principio establece que para un sistema cerrado se cumple 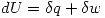 es un diferencial exacto. Esto nos permite escribir que:
es un diferencial exacto. Esto nos permite escribir que:
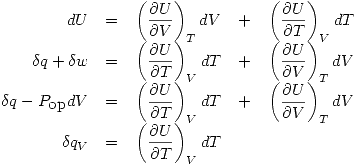
De lo que podemos deducir que 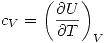
Idénticamentem y definiendo la entalpía: 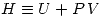 ; se tiene que:
; se tiene que:
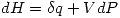 y
y 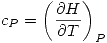
Se halla la relación entre las capacidades caloríficas para un gas ideal como: 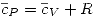 .
.
También para procesos adiabáticos (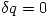 ) para gases ideales se tiene que
) para gases ideales se tiene que 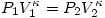 siendo
siendo 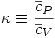
El segundo principio establece que:
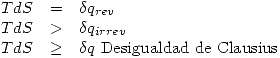
Los procesos espontáneos son irreversibles.
Cambios de entropía
- A P constante:
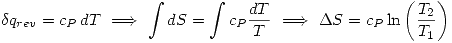
- A V constante: idénticamente:
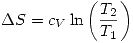
- Durante una transformación de fase:
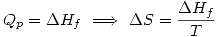
- Para un gas ideal:
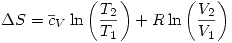
El primer principio permite escribir a las funciones termodinámicas de maneras cómodas que dan lugar a relaciones que llamamos Relaciones de Maxwell:

Existe otra ecuación importante: Ecuación de Gibbs-Helmholtz 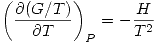
Propiedades Molares Parciales y Sistemas Multicomponentes
Una propiedad molar parcial se define como: 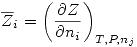
En especial el Potencial químico de un componente en una mezcla es la energía libre molar parcial de ese componente en esa mezcla.
Toda propiedad 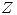 en una mezcla puede escribirse como función de
en una mezcla puede escribirse como función de  ,
,  y la composición. Entonces:
y la composición. Entonces:
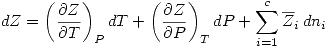
Además 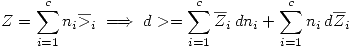 .
.
Igualando: 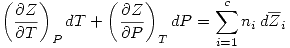 .
.
Es decir: 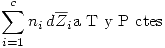 . Esta es la ecuación de Gibbs-Duhein.
. Esta es la ecuación de Gibbs-Duhein.
En un equilibrio de fases los potenciales químicos de cada compuesto son iguales en todas las fases. Esto es: 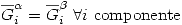
Condiciones de espontaneidad y equilibrio.
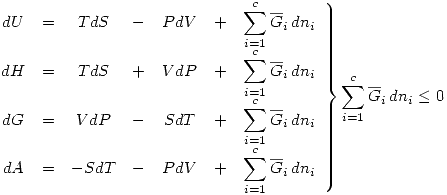
Los Grados de libertad son 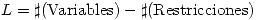 . Para un equilibrio de fases las variables son las composiciones cada componente en cada fase y la temperatura y presión de cada fase. Si tenesmos
. Para un equilibrio de fases las variables son las composiciones cada componente en cada fase y la temperatura y presión de cada fase. Si tenesmos  fases y
fases y  componentes entonces:
componentes entonces: 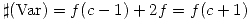 Las restricciones se refieren a equilibrio térmico, mecánico y de fases, es decir:
Las restricciones se refieren a equilibrio térmico, mecánico y de fases, es decir:
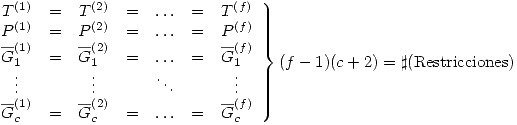
Por lo tanto: 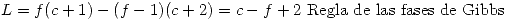
Gases reales
Para un gas ideal 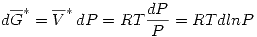 .
.
Pero 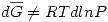 entonces se define la fugacidad tal que:
entonces se define la fugacidad tal que:
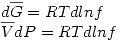
El estado de referencia se define como: 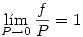
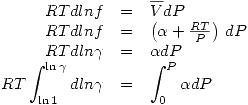
Donde 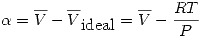 depende del gas en cuestión.
depende del gas en cuestión.
Soluciones
Se define una Propiedad de Mezcla como:
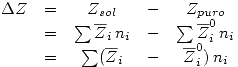
Una Solución Ideal es la que cumple que 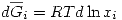
En este tipo de soluciones se cumple:
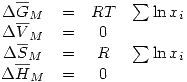
Una solución ideal de gases ideales cumple que:
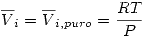
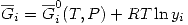
Y además: 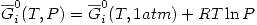
Por lo tanto: 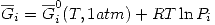
Una solución ideal de gases reales cumple que:
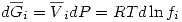
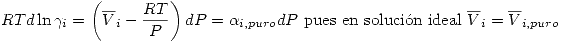
![<tex>RT[ \ln \frac{f_i}{P} - \ln y_i ] =\int_0^P \alpha_i^0dP</tex> <tex>RT[ \ln \frac{f_i}{P} - \ln y_i ] =\int_0^P \alpha_i^0dP</tex>](lib/plugins/latex/images/0320a43a7c02f2c783d94398a21babdece2d175f_0.png)
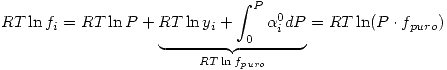
Por lo tanto: 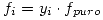 Ley de Lewis-Randall
Ley de Lewis-Randall
Una solución ideal líquida está en equilibrio con su vapor. Consideraremos ese vapor real. Entonces:
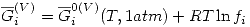
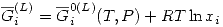
Como en equilibrio 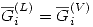 , entonces:
, entonces:
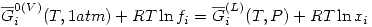
![<tex>RT\ln{x_i}=\underbrace{\overline{G}_i^{0(V)}(T,1atm)-\overline{G}_i^{(L)}(T,P)}_ {RT\ln[f_i^0(T,P_v)]}+RT\ln{f_i}</tex> <tex>RT\ln{x_i}=\underbrace{\overline{G}_i^{0(V)}(T,1atm)-\overline{G}_i^{(L)}(T,P)}_ {RT\ln[f_i^0(T,P_v)]}+RT\ln{f_i}</tex>](lib/plugins/latex/images/def5d57046d925aadac6f20d0fa93982058d511e_0.png)
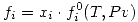
Si el gas fuera ideal:
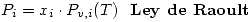
Soluciones reales
En este tipo de soluciones se cumple 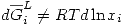 . Entonces se definirá una nueva variable
. Entonces se definirá una nueva variable 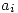 : Actividad del componente i en la solución, que cumple:
: Actividad del componente i en la solución, que cumple: 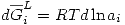
Se definirá un Estado tipo de Raoult diciendo que la actividad raoultiana de un componente puro líquido o sólido a la temperatura y presión del sistema es igual a la unidad, es decir: 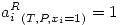
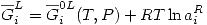
Se definirá también el coeficiente de actividad raoultiano: 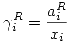
Además:
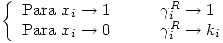
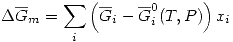
Para una mezcla real:
![<tex>\Delta\overline{G}_m=\sum_i x_i[ \overline{G}_i^0(T,P)+RT\ln{a_i^R}-\overline{G}_i^0(T,P)]</tex> <tex>\Delta\overline{G}_m=\sum_i x_i[ \overline{G}_i^0(T,P)+RT\ln{a_i^R}-\overline{G}_i^0(T,P)]</tex>](lib/plugins/latex/images/cbea41e71433ba583e3600d634fc0339d0227451_0.png)
![<tex>\Delta\overline{G}_m=RT\sum_i x_i\ln{a_i^R}=RT\sum_i x_i [ \ln{\gamma_i^R}+\ln{x_i}]</tex> <tex>\Delta\overline{G}_m=RT\sum_i x_i\ln{a_i^R}=RT\sum_i x_i [ \ln{\gamma_i^R}+\ln{x_i}]</tex>](lib/plugins/latex/images/2159cb65244247dd52f33551ef858aed8307bc26_0.png)
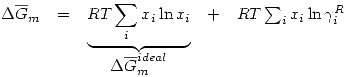
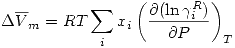
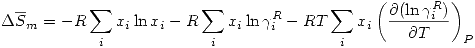
Se define una propiedad de exceso, a la diferencia entre una propiedad y el valor ideal.
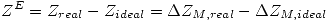
Por ejemplo: 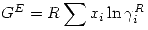
También existe un estado tipo de Henry definido como el estado a T y P del sistema del componente puro extrapolado a dilución infinita. Entonces se cumple:
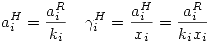
Por lo tanto se cumplen las siguientes relaciones simultáneas:
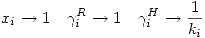
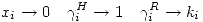
Se cumple para ambas actividades que: 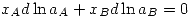
Solución regular
Una solución regular cumple las siguientes propiedades:
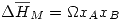
![<tex>\Delta \overline{S}_M=-R[ x_A\ln{x_A} +x_B\ln{x_B}]</tex> <tex>\Delta \overline{S}_M=-R[ x_A\ln{x_A} +x_B\ln{x_B}]</tex>](lib/plugins/latex/images/d0235d0df51cec590ef53ccc68bace642d395a47_0.png)
![<tex>\Delta \overline{G}_M=\Omega x_Ax_B+RT[ x_A\ln{x_A} +x_B\ln{x_B}]</tex> <tex>\Delta \overline{G}_M=\Omega x_Ax_B+RT[ x_A\ln{x_A} +x_B\ln{x_B}]</tex>](lib/plugins/latex/images/52b218a39955995816b425bc18258d6a05fefe52_0.png)
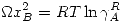
Equilibrio químico
En una reacción general, siendo 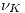 los coeficientes estequimétricos, entonces:
los coeficientes estequimétricos, entonces:
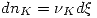
Además en el equilibrio debe cumplirse 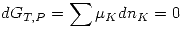
![<tex>dG_{T,P}=\sum (\mu_K^0+RT\ln{a_K}) \nu_K d\xi=\left[ \sum \nu_K\mu_K^0 + RT \ln{\prod a_K^{\nu_K}} \right]d\xi</tex> <tex>dG_{T,P}=\sum (\mu_K^0+RT\ln{a_K}) \nu_K d\xi=\left[ \sum \nu_K\mu_K^0 + RT \ln{\prod a_K^{\nu_K}} \right]d\xi</tex>](lib/plugins/latex/images/9aca6117f461e6633b220b1191cae8ea323a4b1b_0.png)
Se definen: 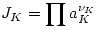 y
y 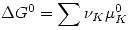
![<tex>dG_{T,P}=\left[ \Delta G^0 +RT\ln{J_K} \right]d\xi</tex> <tex>dG_{T,P}=\left[ \Delta G^0 +RT\ln{J_K} \right]d\xi</tex>](lib/plugins/latex/images/d691393b3af96540fd62efbeb537b04432ccfbb5_0.png)
En el equilibrio entonces:
![<tex>0=\left[ \Delta G^0 +RT\ln{\prod a_{K,eq}^{\nu_K}} \right]d\xi</tex> <tex>0=\left[ \Delta G^0 +RT\ln{\prod a_{K,eq}^{\nu_K}} \right]d\xi</tex>](lib/plugins/latex/images/9f5412dc579ed84ca1ae01842cfc97e41e7a48b5_0.png)
Por lo tanto se define 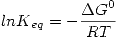 o
o 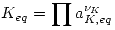
Entonces: 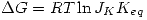 lo que expresa el principio de L'Chatellier.
lo que expresa el principio de L'Chatellier.
Las dependecias del equilibrio son:
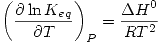
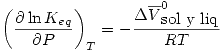 que generalmente es despreciable.
que generalmente es despreciable.
