Examen Final - 63.06. Química Física I
Cátedra: Teresa Estela Pérez
Fecha: 3ª Oportunidad - 1º Cuatrimestre 2004
Día: 28/07/2004
Enunciado
Punto I
En una planta se dispone de 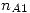 moles de una solución equimolar de los gases A y B, a
moles de una solución equimolar de los gases A y B, a  y
y  . Por razones de proceso es necesario reducir a
. Por razones de proceso es necesario reducir a 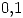 la fracción molar de B, lo cual se lleva a cabo mezclando la solución anterior con gas A puro.
la fracción molar de B, lo cual se lleva a cabo mezclando la solución anterior con gas A puro.
Dado que el gas A está disponible en planta a  y
y 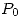 (distinta de
(distinta de  ), antes del mezclado se lo hace pasar por una etapa de compresión isotérmica para llevarlo a
), antes del mezclado se lo hace pasar por una etapa de compresión isotérmica para llevarlo a  , durante este proceso la presión de oposición es constante e igual a
, durante este proceso la presión de oposición es constante e igual a 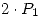 y la temperatura del medio es
y la temperatura del medio es  .
.
Se pide explicar detalladamente (presentando las ecuaciones necesarias y justificando) como procedería al cálculo de:
 ,
,  ,
,  y
y  para la compresión del gas A.
para la compresión del gas A.- El
 que experimenta el sistema en el proceso de mezcla de la solución A y B con el gas A puro. Esta mezcla se lleva a cabo a temperatura y presión constantes y se sabe que los gases forman solución ideal.
que experimenta el sistema en el proceso de mezcla de la solución A y B con el gas A puro. Esta mezcla se lleva a cabo a temperatura y presión constantes y se sabe que los gases forman solución ideal.
Datos:
Las ecuaciones que describen el comportamiento de los gases son:
Gas A: 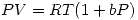 con
con ![<tex>[V]= L\cdot mol^{-1} \quad [b]=atm^{-1}</tex> <tex>[V]= L\cdot mol^{-1} \quad [b]=atm^{-1}</tex>](lib/plugins/latex/images/cb3696a14a11279fd6490110609fafdec31ed871_0.png)
Gas B: 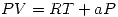 con
con ![<tex>[V] = L/mol \quad [a]= L/mol </tex> <tex>[V] = L/mol \quad [a]= L/mol </tex>](lib/plugins/latex/images/25108bc67c11d54195dfce498b90d6442853ded6_0.png)
Punto II
Para un sistema gaseoso de moléculas diatómicas indicar:
- Cuáles son los grados de libertad para las distintas formas de energía que posee la molécula.
- Como se relaciona la función de partición molecular con las formas de energía que posee esa molécula.
¿Cómo cambia lo pedido en los puntos anteriores si la molécula es triatómica lineal?
Resolución
Punto I
Parte 1
Para la compresión primero voy a calcular la cantidad de gas A puro 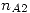 necesario. Esto es:
necesario. Esto es:
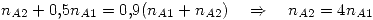
Ahora vemos que: 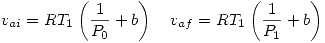
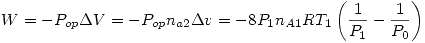
![<tex>dU = NC_V\underbrace{dT}_{=0} + \left( \frac{\partial U}{\partial V} \right)_TdV = \left[ T\underbrace{\left( \frac{\partial S}{\partial V} \right)_T}_{\mbox{R. de Maxwell}} -P \right]dV=\left[ T \left( \frac{\partial P}{\partial T} \right)_V -P \right]dV</tex> <tex>dU = NC_V\underbrace{dT}_{=0} + \left( \frac{\partial U}{\partial V} \right)_TdV = \left[ T\underbrace{\left( \frac{\partial S}{\partial V} \right)_T}_{\mbox{R. de Maxwell}} -P \right]dV=\left[ T \left( \frac{\partial P}{\partial T} \right)_V -P \right]dV</tex>](lib/plugins/latex/images/661635d94d3af882128cdb6495d7a487ba559fd5_0.png)
Entonces debemos evaluar la derivada de la presión en la ecuación de estado de A:
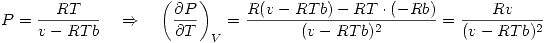
![<tex>T \left( \frac{\partial P}{\partial T} \right)_V -P = \frac{RTv}{(v-RTb)^2}-\frac{RT}{v-RTb}=\frac{RT}{v-RTb} \left[ \frac{v}{v-RTb} -1 \right]</tex> <tex>T \left( \frac{\partial P}{\partial T} \right)_V -P = \frac{RTv}{(v-RTb)^2}-\frac{RT}{v-RTb}=\frac{RT}{v-RTb} \left[ \frac{v}{v-RTb} -1 \right]</tex>](lib/plugins/latex/images/fc4a3b9bcc0bc4c4900560485e045bc7fe15dd98_0.png)
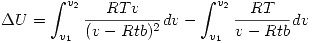
![<tex>\Delta U= \left[-\frac{RTb}{v-RTb}+\ln (v-RTb)\right]_{v_1}^{v_2} -RT \left[\ln(v-RTb)\right]_{v_1}^{v_2}</tex> <tex>\Delta U= \left[-\frac{RTb}{v-RTb}+\ln (v-RTb)\right]_{v_1}^{v_2} -RT \left[\ln(v-RTb)\right]_{v_1}^{v_2}</tex>](lib/plugins/latex/images/62b9761fc9486d65f55636be32c0f99a8e8e6178_0.png)
El calor se despeja del primer principio: 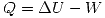
Ahora evaluamos la entalpía: ![<tex>dH=NC_PdT+\left(\frac{\partial H}{\partial P}\right)_TdP=\left[v-T\left( \frac{\partial v}{\partial T}\right)_P \right]dP</tex> <tex>dH=NC_PdT+\left(\frac{\partial H}{\partial P}\right)_TdP=\left[v-T\left( \frac{\partial v}{\partial T}\right)_P \right]dP</tex>](lib/plugins/latex/images/d81b72518c24266600d8e0a0a51287777a2a7975_0.png)
Pero como 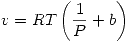 entonces
entonces 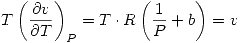 . Por lo tanto
. Por lo tanto 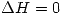
Parte 2
Se mezcla la solución con el A puro, formando una solución ideal. Por definición en una solución ideal se cumple 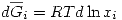
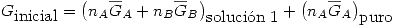
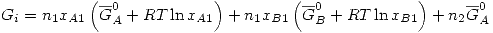
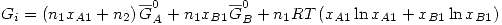
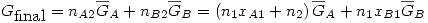
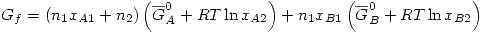
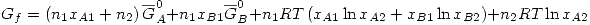
Entonces:
![<tex>G_f -G_i =n_1 RT \left[ x_{A1}\ln{\frac{x_{A2}}{x_{A1}}}+x_{B1}\ln{\frac{x_{B2}}{x_{B1}}} \right] +n_2RT\ln{x_{A2}}</tex> <tex>G_f -G_i =n_1 RT \left[ x_{A1}\ln{\frac{x_{A2}}{x_{A1}}}+x_{B1}\ln{\frac{x_{B2}}{x_{B1}}} \right] +n_2RT\ln{x_{A2}}</tex>](lib/plugins/latex/images/910f75f7355c23a02aa4670fd6a1c1165b1d4a3a_0.png)
Reemplazo por los datos del enunciado:
![<tex>\Delta G=n_{A1}RT_1 \left[ 0.5 \ln{\frac{0.9}{0.5}}+0.5 \ln{\frac{0.1}{0.5}} \right] +4n_{A1}RT_1\ln{0.9}</tex> <tex>\Delta G=n_{A1}RT_1 \left[ 0.5 \ln{\frac{0.9}{0.5}}+0.5 \ln{\frac{0.1}{0.5}} \right] +4n_{A1}RT_1\ln{0.9}</tex>](lib/plugins/latex/images/98a677ff0808cacb2a245dc37219227908a7eb96_0.png)
![<tex>\Delta G=n_{A1}RT_1 \left[ 0.5 \ln{\frac{0.09}{0.25}}+4 \ln{0.9} \right]</tex> <tex>\Delta G=n_{A1}RT_1 \left[ 0.5 \ln{\frac{0.09}{0.25}}+4 \ln{0.9} \right]</tex>](lib/plugins/latex/images/05519c76de338a1a53aa0e30c4053070ff5b2549_0.png)
![<tex>\Delta G=n_{A1}RT_1 \ln \left[ 0.9^4 \sqrt{\frac{0.09}{0.25}} \right]</tex> <tex>\Delta G=n_{A1}RT_1 \ln \left[ 0.9^4 \sqrt{\frac{0.09}{0.25}} \right]</tex>](lib/plugins/latex/images/6fb2802b0a78e44e68d415b1096b40168edc841d_0.png)
Punto II
En un sistema cualquiera la energía total es la suma de las contribuciones energéticas siguientes:
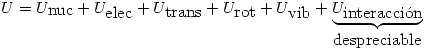
Vamos a contestar la primer pregunta directamente para ambos tipos de moléculas: diatómicas, y triatómicas lineales.
- Nuclear: en ambos casos está formada por las energías de ambos núcleos.
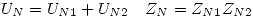
- Electrónica: Generalmente la energía electrónica de cada átomo es la energía electrónica del primer nivel del átomo, pues las de los niveles superiores son despreciables, entonces:
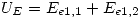
- Translacional: En este caso los grados de libertad de translación son 3 para ambos tipos de moléculas, y todos se engloban en un sólo
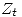 .
. - Rotacional: En este caso los grados de libertad de ambos tipos de moléculas son dos, por ser ambas lineales. Estos ejes de rotación serán dos ejes perpendiculares entre sí, y perpendiculares al eje de la molécula.
- Vibracional: Para un oscilador compuesto lineal la cantidad de grados de libertad de virbación es
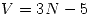 , por lo tanto la molécula diatómica tendrá 1 sólo grado de libertad de vibración
, por lo tanto la molécula diatómica tendrá 1 sólo grado de libertad de vibración  , y la triatómica tendrá 4
, y la triatómica tendrá 4 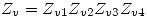 .
.
En todos los casos la función de partición se relaciona con la energía mediante: 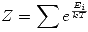 , lo que también puede escribirse usando funciones de partición para cada energía como
, lo que también puede escribirse usando funciones de partición para cada energía como  . En este caso:
. En este caso: