Examen Final - 63.06. Química Física I

Examen Final - 63.06. Química Física I

Cátedra: Teresa Pérez
Fecha: 2ª Oportunidad - Segundo Cuatrimestre 2002
Día: 18/12/2002

Enunciado

En un reactor se desea obtener el producto E mediante la reacción: $<tex>A(l)+2B(l)+C(g) \rightleftharpoons D(l)+3E(g)</tex>$

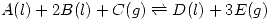
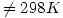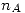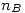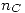El reactor opera a $<tex>P_1</tex>$ y $<tex>T_1</tex>$ ( $<tex>\not= 298K</tex>$ ) y es alimentado por una corriente que contiene $<tex>n_A</tex>$ , $<tex>n_B</tex>$ y $<tex>n_C</tex>$ moles de los reactivos.

Detalle como calcularía la cantidad máxima de E que es posible obtener en esas condiciones de operación.
¿Qué variables modificaría para aumentar la cantidad de E obtenida? Justifique.

Datos:

C y E forman una solución ideal de gases reales y se conocen las temperaturas y presiones criticas de cada uno de los gases puros.
A y D forman una solución de comportamiento regular. Se determino que al formar una solución equimolar de A y D a temperatura y presión constante, a partir de los líquidos puros, el calor intercambiado entre sistema y medio fue de –400cal.
El liquido B es inmiscible con la solución que forman A y D.
Los gases presentan una muy baja solubilidad y puede despreciarse el contenido de A, B y D en la fase gaseosa.
Se sabe que el $<tex>\Delta H_{\mbox{Reacci\'on}} <0</tex>$
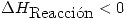
Cuenta con las tablas con datos termodinámicos de los compuestos puros.

Tiempo de resolución: 1 hora.

Observación: Debe hacerse una presentación detallada de cada paso de cálculo, indicando los datos necesarios en cada caso y como obtenerlos.

Resolución

La idea es nombrar los pasos que deberían hacerse para hallar la cantidad de sustancia E que habrá en el equilibrio.

	A(l)	2 B(l)	C(g)	D(l)	3 E(g)
Inicial	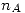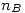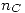$<tex>n_A</tex>$	$<tex>n_B</tex>$	$<tex>n_C</tex>$	-	-
Equilibrio	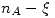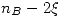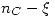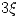$<tex>n_A-\xi</tex>$	$<tex>n_B-2\xi</tex>$	$<tex>n_C-\xi</tex>$	$<tex>\xi</tex>$	$<tex>3\xi</tex>$

De aquí despejaremos las concentraciones en el equilibrio (B es inmiscible en A y D, por lo que no afecta a la concentración):

$<tex>x_A=\frac{n_A-\xi}{n_A} \quad x_D=\frac{\xi}{n_A}</tex>$

$<tex>y_C=\frac{n_C-\xi}{n_c+2\xi} \quad y_E=\frac{3\xi}{n_C+2\xi}</tex>$

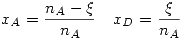
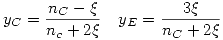
La expresión para la constante de equilibrio en este caso está dada por: 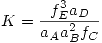$<tex>K=\frac{f_E^3a_D}{a_Aa_B^2f_C}</tex>$

Del dato 1, vemos que: 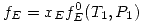$<tex>f_E=x_Ef_E^0(T_1,P_1)</tex>$ y $<tex>f_C=x_Cf_C^0(T_1,P_1)</tex>$ .

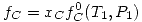Del dato 3 observamos que 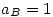$<tex>a_B=1</tex>$ .

El dato dos se interpreta sabiendo que el calor de disolución para una solución regular es 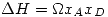$<tex>\Delta H=\Omega x_Ax_D</tex>$ . Utilizando los datos de allí, despejamos $<tex>\Omega =-1600\mbox{cal}</tex>$ .

$<tex>RT\ln{\gamma_A^R}=\Omega x_D^2 \quad \rightarrow a_A^R=x_A e^{\frac{\Omega}{RT}x_D^2}</tex>$

$<tex>K=\frac{y_E^3{f_E^0}^3\gamma_D^Rx_D}{\gamma_A^Rx_Ay_cf_C^0}=\frac{y_E^3x_D}{x_Ay_C}\cdot \frac{{f_E^0}^3}{f_C^0}e^{\frac{\Omega}{RT}(x_A^2-x_D^2)}</tex>$

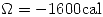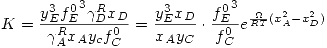
Determinación de K
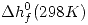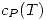Con los datos termodinámicos de $<tex>\Delta h_f^0(298K)</tex>$ y $<tex>c_P(T)</tex>$ se hallan: 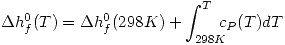$<tex>\Delta h_f^0(T)=\Delta h_f^0(298K)+\int_{298K}^{T}\!\!\!\!c_P(T)dT</tex>$ . Si ocurriese un cambio de estado en realidad debería aplicar la fórmula 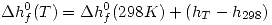$<tex>\Delta h_f^0(T)=\Delta h_f^0(298K)+(h_T-h_{298})</tex>$ (Suponiendo P suficientemente baja).

Luego se halla 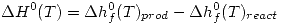$<tex>\Delta H^0(T)=\Delta h_f^0(T)_{prod}-\Delta h_f^0(T)_{react}</tex>$

$<tex>\left( \frac{\partial \ln{K}}{\partial T} \right)_P=\frac{\Delta H^0}{RT^2}</tex>$

$<tex>\Rightarrow \ln{\frac{K}{K_{298}}}=\frac{1}{R}\int_{298K}^{T}\frac{\Delta H^0(T)}{T^2}dT</tex>$

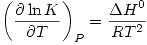
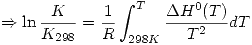
Determinación de las fugacidades para E y C

$<tex>RTd\ln{\frac{f_i^0}{P}}=\left( v-\frac{RT}{P} \right) dP</tex>$

$<tex>d\ln{\frac{f_i^0}{P}}=\left( \frac{v}{RT}-\frac{1}{P} \right) dP = \left( \frac{Z-1}{P} \right) dP</tex>$

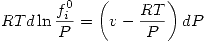
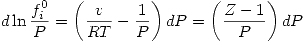
Entonces: 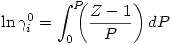$<tex>\ln{\gamma_i^0}=\int_0^P \!\!\!\! \left( \frac{Z-1}{P} \right) dP </tex>$

Esta integral debe resolverse gráficamente usando los valores reducidos de E y C. De aquí se podría despejar 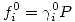$<tex>f_i^0=\gamma_i^0P</tex>$

Ahora entonces ya se pudo calcular K y los datos de las fugacidades. Por lo tanto reemplazando los datos en la fórmula antes hallada queda:

$<tex>K=\frac{27\xi^4}{(n_A-\xi)(n_C-\xi)(n_c+2\xi)^2}\cdot\frac{{f_E^0}^3}{f_C^0}\cdot e^{\frac{\Omega}{RT}\left( 1-\frac{2}{n_A}\xi \right)}</tex>$

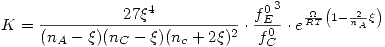
En esta ecuación ya son todos datos, excepto $<tex>\xi</tex>$ . Entonces debería despejarlo (o aproximarlo mediante iteraciones).

Una vez que haga eso la cantidad de E en el equilibrio es 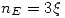$<tex>n_E=3\xi</tex>$

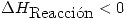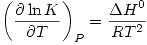La parte 2 que pregunta que variables modificaría para mejorar el rendimiento. Una podría ser disminuír la temperatura, pues como el dato 5 dice que $<tex>\Delta H_{\mbox{Reacci\'on}} <0</tex>$ y $<tex>\left( \frac{\partial \ln{K}}{\partial T} \right)_P=\frac{\Delta H^0}{RT^2}</tex>$ , entonces 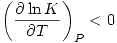$<tex>\left( \frac{\partial \ln{K}}{\partial T} \right)_P <0</tex>$ . Por lo tanto una disminución de la temperatura aumentaría el valor de K, y por lo tanto aumentaría el rendimiento.

Discusión

Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá o mandáme un mail GastonK