Examen Parcial - 62.15. Física IIID - 22/09/2008
Cátedra: María Alejandra Aguirre/002
Fecha: Primera Oportunidad - (Segundo Cuatrimestre) 2008
Día: 22/09/2008
Enunciado
Punto I
Se irradia un metal de función trabajo  con radiación de
con radiación de 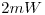 de potencia, emitida por un gas de átomos cuyos electrones decaen de un nivel con
de potencia, emitida por un gas de átomos cuyos electrones decaen de un nivel con  a otro con
a otro con  . El potencial de frenado del flujo fotoeléctrico es
. El potencial de frenado del flujo fotoeléctrico es  . Determinar:
. Determinar:
- El rango de energía cinética que poseen los fotoelectrones.
- La función de trabajo
 .
. - La intensidad de corriente si el rendimiento fotoeléctrico es
 .
.
Punto II
En un microscopio electrónico los electrones son acelerados mediante un voltaje  a fin de obtener una longitud de onda adecuada para detectar objetos pequeños. La longitud de onda debe ser menor que el tamaño del objeto. Si se quiere observar un virus, derivar la expresión para el voltaje
a fin de obtener una longitud de onda adecuada para detectar objetos pequeños. La longitud de onda debe ser menor que el tamaño del objeto. Si se quiere observar un virus, derivar la expresión para el voltaje  requerido a fin de obtener una longitud de onda de de Broglie 1000 veces más pequeña que
requerido a fin de obtener una longitud de onda de de Broglie 1000 veces más pequeña que 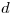 , el tamaño del virus (suponer el movimiento del electrón como no relativista).
, el tamaño del virus (suponer el movimiento del electrón como no relativista).
Punto III
Una partícula responde a una función de onda cuya parte espacial ( ) se esquematiza en la figura.
) se esquematiza en la figura.
- Indicar cualitativamente la relación entre la energía
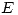 con la que incide la partícula y la energía potencial
con la que incide la partícula y la energía potencial  . Esquematizar ambas indicando de qué dirección incide la partícula. Justificar.
. Esquematizar ambas indicando de qué dirección incide la partícula. Justificar. - Escribir la función de onda para todo x y todo t. (Durante el parcial se explico que no se pedía resolver el sistema de ecuaciones, que había que dejar la función expresada en función de constantes y plantear las ecuaciones que surgen de las condiciones de contorno)
- Encontrar una expresión general para la probabilidad
 de encontrar a la partícula en la región
de encontrar a la partícula en la región  .
.
Punto IV
La emisión de radiación en un átomo se puede estimular por medio de una fuente de radiación o por bombardeo con electrones. Si un gas de hidrógeno (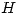 ) se encuentra en su estado fundamental:
) se encuentra en su estado fundamental:
- Explicar detalladamente lo que ocurre cuando incide radiación de
 Å sobre los átomos de
Å sobre los átomos de 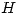 y calcule las líneas de emisión que se observan. Hacer un diagrama de todas las transiciones involucradas.
y calcule las líneas de emisión que se observan. Hacer un diagrama de todas las transiciones involucradas. - Idem si se incide con electrones de igual energía que la radiación del punto anterior.
Resolución
Punto I
1)
Para calcular el rango de energía cinética hay que calcular la máxima, ya que la mínima es  .
.
 Por lo tanto el rango de energías es
Por lo tanto el rango de energías es ![<tex>[0,6]eV</tex> <tex>[0,6]eV</tex>](lib/plugins/latex/images/45dd8958c9ba457320da2dface40c1eaf51d7fb7_0.png) .
.
2)
Cuando se produce el efecto fotoeléctrico se cumple la siguiente relación  . Cuando se desprenden electrones del borde de la superficie, no se pierde energía disipada en forma de calor, por lo que la energía cinética es la máxima. Aplicando esto último y despejando de la ecuación queda
. Cuando se desprenden electrones del borde de la superficie, no se pierde energía disipada en forma de calor, por lo que la energía cinética es la máxima. Aplicando esto último y despejando de la ecuación queda  , donde
, donde  y
y  es la calculada en el punto anterior.
es la calculada en el punto anterior.
Entonces  .
.
3)
Lo que se pide calcular es la corriente, es decir “carga por unidad de tiempo”, que como son electrones es igual a “número de e-'s por unidad de tiempo“*
Por otro lado, “número de e-'s por unidad de tiempo”  *”número de fotones por unidad de tiempo”.
*”número de fotones por unidad de tiempo”.
Además,  = “cantidad de energía por unidad de tiempo” = “número de fotones por unidad de tiempo“*
= “cantidad de energía por unidad de tiempo” = “número de fotones por unidad de tiempo“* , donde
, donde  como se calculó en el punto anterior.
como se calculó en el punto anterior.
De esta última ecuación se obtiene “número de fotones por unidad de tiempo” 
“número de e-'s por unidad de tiempo” 
Por último 
Punto II
Por un lado, la energía cinética de los e-'s al aplicar un potencial de aceleración  es
es  .
.
Por otro lado,  y por de Broglie,
y por de Broglie,  .
.
Reemplazando 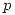 e igualando las expresiones, se tiene
e igualando las expresiones, se tiene  .
.
Ahora, se quiere  , entonces
, entonces  y de esta expresión se despeja
y de esta expresión se despeja 
Punto III
1)
En el gráfico de la función de onda se pueden ver los siguientes puntos:
- En la región II la función de onda es exponencial lo que indica efecto túnel
 .
. - Además el máximo en esta región se encuentra en
 La partícula incide desde la izquierda.
La partícula incide desde la izquierda. - En las regiones I y III se tiene una onda
 y
y  .
. - Durante el parcial se aclaró que
 en las regiones I y III era el mismo. Como
en las regiones I y III era el mismo. Como  depende de
depende de 
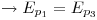 .
.
Juntando todos esos puntos:
2)
En primer lugar,  es constante en todas las regiones, por lo que
es constante en todas las regiones, por lo que  y
y 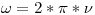 .
.
Región I) 
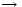
 es un número complejo,
es un número complejo,  y
y  .
.
 . Como la partícula se mueve de izquierda a derecha, al llegar a
. Como la partícula se mueve de izquierda a derecha, al llegar a  parte de la onda puede rebotar, entonces
parte de la onda puede rebotar, entonces 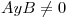
Región II) 
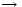
 es un número real,
es un número real,  y
y  .
.
 . Como la región es acotada, ninguna de las dos exponenciales diverge dentro de la región 2, entonces
. Como la región es acotada, ninguna de las dos exponenciales diverge dentro de la región 2, entonces 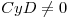 .
.
Región III) 
 es un número complejo,
es un número complejo,  y
y  .
.
 . Como la partícula ya no puede rebotar porque no se producen mas cambios de potencial
. Como la partícula ya no puede rebotar porque no se producen mas cambios de potencial  .
.
La función  va a estar dividida en 3 regiones y en cada una
va a estar dividida en 3 regiones y en cada una 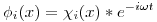
Condiciones de contorno:



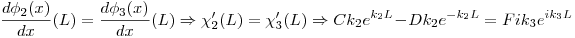

3)
 Esta integral no converge.
Esta integral no converge.

Punto IV
1)
Al incidir con radiación en un gas, los fotones pueden excitar a los átomos (de 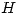 en este caso) si poseen la cantidad de energía necesaria. Si se produce la excitación, al cabo de un tiempo los e-'s van a volver al estado fundamental, emitiendose fotones de distintas longitudes de onda según el tipo de salto que se produzca.
en este caso) si poseen la cantidad de energía necesaria. Si se produce la excitación, al cabo de un tiempo los e-'s van a volver al estado fundamental, emitiendose fotones de distintas longitudes de onda según el tipo de salto que se produzca.
Para excitar a un átomo, el fotón debe perder toda su energía, si no no hay interacción. Los niveles de energía para un átomo de 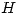 están dados por
están dados por  :
:
Los fotones tienen  . Entonces, para que se excite un átomo de
. Entonces, para que se excite un átomo de 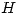 que se encuentra inicialmente en el estado fundamental, debe existir un nivel con energía tal que
que se encuentra inicialmente en el estado fundamental, debe existir un nivel con energía tal que  , es decir, un nivel con energía
, es decir, un nivel con energía  . Pero en el esquema se ve que no hay ningún nivel con esta energía, por lo que no se excita el gas y no se emiten fotones.
. Pero en el esquema se ve que no hay ningún nivel con esta energía, por lo que no se excita el gas y no se emiten fotones.
2)
A diferencia de los fotones, cuando se bombardea con e-'s estos si pueden perder parte de su energía cinética, por lo que existe una probabilidad de que se produzcan todos los saltos que requieran menor energía que la que poseen el e-.
De esta forma los posibles saltos que puede realizar el e- del nivel fundamental son a n=2 ( ) y n=3 (
) y n=3 ( ). Para n=4 se requieren 12,75eV entonces este salto no es posible.
). Para n=4 se requieren 12,75eV entonces este salto no es posible.
Como el átomo va a pasar a un estado excitado, va a caer nuevamente al estado fundamental, emitiendo un fotón. Las posibles caídas son:

Si el e- pasó al nivel n=3, puede caer directamente a n=1 o primero caer a n=2 y luego a n=1. Si pasó a n=2 al ser excitado, sólo puede caer a n=1. En cada salto se emite un fotón con 
Entonces, las posibles lineas de emisión son 3:
 Å
Å Å
Å
 Å
Å Å
Å
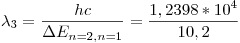 Å
Å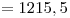 Å
Å



