Examen Parcial - 62.15 Física III D
Cátedra: Arcondo
Fecha: 1° Recuperatorio - 1° Cuatrimestre
Día: 13/06/2006
Enunciado
Punto I
Un haz de rayos 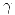 de una fuente de 137Cs con
de una fuente de 137Cs con 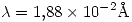 incide sobre un electrón en reposo. Si la radiación dispersada por efecto Compton se detecta a 90° del haz incidente. Obtener:
incide sobre un electrón en reposo. Si la radiación dispersada por efecto Compton se detecta a 90° del haz incidente. Obtener:
- El cambio en la longitud de onda.
- La energía cinética que adquiere el electrón dispersado.
- La cantidad de movimiento lineal del electrón dispersado en la dirección perpendicular a la del fotón incidente. Dar el resultado en km m/s.
Punto II
Un gas de hidrógeno en el estado fundamental se excita mediante un haz de fotones, alcanzado un estado con momento angular 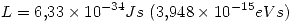 . Teniendo en cuenta el modelo de Bohr:
. Teniendo en cuenta el modelo de Bohr:
- Indique la máxima longitud de onda posible de los fotones incidentes.
- Indique cuántas líneas se observan en el espectro visible.
- Realice un esquema de los niveles de energía y de todas las transiciones posibles que se emitan en el ultravioleta.
Punto III
Un electrón se encuentra en el tercer estado excitado de un pozo infinito de 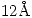 de ancho.
de ancho.
- ¿Cuál es la probabilidad de encontrarlo entre
 y
y 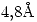 ? ¿Y entre
? ¿Y entre  y
y 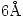 ?
? - ¿En qué entornos es más probable encontrar al electrón?
- ¿Cuál es el valor medio del impulso lineal p del electrón?
Punto IV
Para una caja de lados  y
y 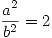 obtener la energía de los tres niveles más bajos. Si dicha caja contuviera 11 electrones:
obtener la energía de los tres niveles más bajos. Si dicha caja contuviera 11 electrones:
- Hacer un esquema energético de los electrones en el sistema. Calcular los niveles de energía e indicar su degeneración. Calcular la energía del estado fundamental en este caso.
- ¿Cuál es la energía de Fermi?
- Repetir los puntos 1 y 2 para el caso de tener la caja en presencia de un campo magnético
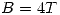 .
.
Resolución
Punto I
1)
Para calcular el cambio en la longitud de onda utilizaremos la ecuación de Compton:
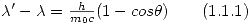
Reemplazando los valores queda:
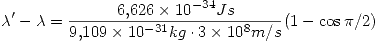

2)
Comenzamos planteando conservación de la energía:
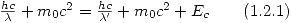
Esto es: la energía del fotón incidente más la energía de masa en reposo del electrón, debe ser igual a la energía del fotón dispersado, más la energía de masa en reposo del electrón más la energía cinética adquirida por este último. Antes de seguir calcularemos la longitud de onda del fotón dispersado:
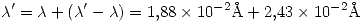
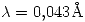
Despejando la ecuación (1.2.1) para 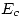 tenemos:
tenemos:
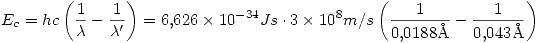
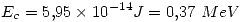
3)
En este punto nunca escribir 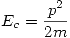 , pues en una experiencia de Compton es muy probable que existan apreciables efectos relativistas. En todo caso, esa ecuación puede escribirse pero teniendo en cuenta la masa corregida y no la del electrón en reposo. De todas formas, para resolver este ejercicio, vamos a plantear conservación de la cantidad de movimiento del sistema fotón-electrón:
, pues en una experiencia de Compton es muy probable que existan apreciables efectos relativistas. En todo caso, esa ecuación puede escribirse pero teniendo en cuenta la masa corregida y no la del electrón en reposo. De todas formas, para resolver este ejercicio, vamos a plantear conservación de la cantidad de movimiento del sistema fotón-electrón:
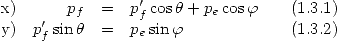
El segundo miembro de la ecuación (1.3.2) es igual a la componente en y del momento lineal del electrón. Evaluamos para obtener el valor de 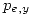 :
: