Examen Final - 62.15 Física III D
- Enunciado
  - Punto 1
  - Punto 2
  - Punto 3
  - Punto 4
  - Punto 5
  - Punto 6
- Resolución
  - Punto 5
  - Punto 6
- Discusión

Examen Final - 62.15 Física III D

Cátedra: Arcondo
Día: 28/12/2006

Explicar por que razón la probabilidad de que se presente efecto Compton en la interacción de la radiación con la materia aumenta con la energía de la radiación. Graficar el espectro de la radiación dispersada a 90º de la dirección de incidencia y explicarlo brevemente.

Punto 2

Una onda de materia incide desde la derecha sobre un escalón de potencial, la energía potencial de la particula es E < 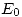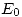$<tex>E_0</tex>$ ( $<tex>E_0</tex>$ = Energía del escalón). La probabilidad de penetración en el escalón es no nula. Analizar brevemente que pasa con la energía cinética de la particula en este caso.

Punto 3

El calcio (Z= 20) y el manganeso (Z=25) tienen ambos dos electrones 4s de valencia pero tienen un comportamiento magnético muy diferente. Analizarlos tomando en consideración su estructura electrónica.

Punto 4

Los electrones libres en un metal son representados en la teoría cuántica como un gas ideal de electrones sometidos a un pozo infinito de potencial. Que otras hipótesis se consideran? Que representa la energía de Fermi del metal?

Punto 5

Una oblea de Si (Eg = 1,12 eV) está dopada con P. La concentración de impurezas es 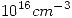$<tex>10^{16} cm^{-3}</tex>$ y su energía de ionización es 45 meV. A 300 K, la concentración intrínseca es 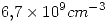$<tex>6.7 \times 10^{9} cm^{-3}</tex>$ , la concentración efectiva de estados en la banda de conducción es Nc = $<tex>2.8 \times 10^{19} cm^{-3}</tex>$ y la concentración efectiva de estados en la banda de valencia es Nv= $<tex>1.04 \times 10^{19} cm^{-3}</tex>$ . 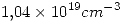Estimar la energía de Fermi y trazar un esquema de bandas a T = 300 K. Justificar.

Punto 6

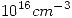Una juntura NP esta formada por Si dopado con P y Si dopado con B ( $<tex>E_i = 45 meV</tex>$ ). La concentración de impurezas es $<tex>10^{16} cm^{-3}</tex>$ en ambos casos. Hallar el potencial de contacto a 300 K. Estimar el ancho de la zona de agotamiento. Si se la polariza en directa con un potencial $<tex>V_0</tex>$ analizar que pasa con el ancho de la zona de agotamiento.