Tabla de Contenidos
2º Parte Evaluación Parcial - 61.09. Electromagnetismo B
Fecha: Segunda Parte - 1er Cuatrimestre 2013
Día: 11/05/2013
Esta página está incompleta; podés ayudar completando el material.
Enunciado
- Electrodinámica
- En una región del espacio donde hay un campo uniforme
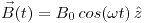 se coloca una espira rígida, cuadrada de lado
se coloca una espira rígida, cuadrada de lado  , contenida en el plano
, contenida en el plano 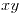 .
.- Dibujar en una misma gráfica las variaciones en el tiempo de
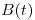 y de la fem inducida sobre la espira.
y de la fem inducida sobre la espira. - Repita la gráfica si ahora además la espira se mueve con velocidad constante en una dirección normal a
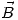 .
.
- Por un solenoide muy largo de N espiras y radio
 circula una corriente
circula una corriente 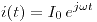 . En el centro del mismo hay una espira concéntrica de radio
. En el centro del mismo hay una espira concéntrica de radio 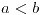 y resistencia
y resistencia  . Hallar:
. Hallar:- Los campos eléctrico y magnético en el interior del solenoide a primer orden en la aproximación cuasi-estática.
- La potencia disipada por efecto Joule en la espira a partir de los campos calculados.
- Lineas de transmisión
- Defina y explique el significado de los coeficientes de reflexión y transmisión sobre la carga para una linea cargada. Determine la impedancia de entrada si la línea tiene una longitud
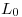 . ¿Se puede lograr que una línea con pérdidas conectada a una carga compleja presente una impedancia de entrada real? Explique.
. ¿Se puede lograr que una línea con pérdidas conectada a una carga compleja presente una impedancia de entrada real? Explique. - Una línea de transmisión de impedancia característica de
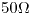 conecta una fuente de tensión senoidal de frecuencia
conecta una fuente de tensión senoidal de frecuencia  con una carga de impedancia
con una carga de impedancia 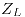 . La longitud de la línea para dicha frecuencia es de
. La longitud de la línea para dicha frecuencia es de 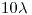 y se verifica que el valor mínimo de tensión (pico) sobre la línea es de
y se verifica que el valor mínimo de tensión (pico) sobre la línea es de 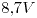 , y el primer máximo de tensión (pico) de
, y el primer máximo de tensión (pico) de 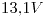 se encuentra a una distancia
se encuentra a una distancia 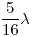 de la carga. Se pide:
de la carga. Se pide:- Calcular el valor del coeficiente de reflexión sobre la carga y el valor de
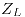 .
. - Hallar la expresión del valor instantáneo de la corriente en el centro de la línea.
- Diseñe un adaptador de cuarto de onda para adaptar la carga.
Resolución
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
