Tabla de Contenidos
1º Parte Evaluación Parcial - 61.09. Electromagnetismo B
Fecha: Primera Parte - 1er Cuatrimestre 2013
Día: 13/04/2013
Esta página está incompleta; podés ayudar completando el material.
Enunciado
- Campos Cuasiestáticos
- Defina los conceptos de autoinductancia e inductancia mutua y explique justificadamente sus propiedades.
- Enuncie las propiedades básicas de la teoría del potencial y demuestre al menos una de ellas.
- Considere un solenoide corto con
 vueltas por unidad de longitud y radio
vueltas por unidad de longitud y radio  . A una distancia
. A una distancia 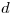 y sobre el eje del solenoide se encuentra una espira de radio
y sobre el eje del solenoide se encuentra una espira de radio  mucho más pequeño que
mucho más pequeño que  . Calcule la inductancia mutua entre el solenoide y la espira de la forma más precisa que se le ocurra, justificando su elección.
. Calcule la inductancia mutua entre el solenoide y la espira de la forma más precisa que se le ocurra, justificando su elección.
- Corrientes estacionarias
- Demuestre la ecuación que describe la conservación de la carga eléctrica
- Para el resistor esférico de la figura, encuentre el potencial, el campo eléctrico y la corriente en el espacio entre
 y
y  . Analice el comportamiento de las magnitudes físicas esenciales en la interfaz de radio
. Analice el comportamiento de las magnitudes físicas esenciales en la interfaz de radio  . Calcule la resistencia de la estructura.*
. Calcule la resistencia de la estructura.*
*Ayuda: Piense cuidadosamente en las condiciones de contorno, propiedades del potencial y los campos en la interfaz. Considere también que está modelando una situación de corriente continua, con lo cual las derivadas temporales de cualquier cantidad son cero.
Resolución
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported


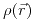 o otro una polarización
o otro una polarización 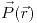 . Plantee todas las formas en la que se puede encontrar el campo electrostático que crean los cuerpos.
. Plantee todas las formas en la que se puede encontrar el campo electrostático que crean los cuerpos.