1. Un eje esta empotrado en sus dos extremos. Sobre el mismo se encuentran dos volantes de momentos de inercia e . La parte del eje situada entre los dos volantes tiene una constante de rigidez rotacional =10⁶ N.m, mientras uqe para el resto es =5.10⁵ N.m. Los momentos polares de inercia de los discos son =10kg.m², =20kg.m². (Recuerde que la energia potencial es la suma de terminos del tipo )

(a )Calcular las frecuencias naturales y los autovectores asociados.
(b )Hallar la matriz modal y los modos normales de vibracion.
(c )Calcular la energia del sistema si 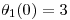grados sexagesimales,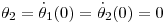

2. Una particula de masa se encuentra en reposo sobre la cima de una esfera de radio . La superficie es sin rozamiento y la unica fuerza que actua es la gravedad. Una muy ligera perturbacion provoca que la particula empiece a deslizar por la esfera:

(a )Usando multiplicadores de lagrange demostrar que el angulo donde la particula se separa de la esfera es tal que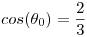

(b )Idem punto anterior pero usando Newton y conservacion de la energia.

(c ) suponga ahora que existe un coeficiente de rozamiento 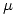entre la esfera y la particula, usando Lagrange demuestra que el angulo de separacion sigue siendo el mismo.

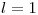3. Una rueda de molino de masa kg y radio m rueda sobre un circulo de radio m.
El tiempo que tarda la rueda en recorrer ese circulo es de 20s.

(a )Calcular el momentoangular de la rueda respecto del centro de coordenadas incerciales y la cupla respectiva.
(b )Calcular la fuerza que ejerce el piso sobre la rueda.