Examen Parcial - 62.03./62.04. Física II - 30/06/2012

Cátedra: Para todas las cátedras
Fecha: 1º Oportunidad - 1º Cuatrimestre 2012
Día: 30/06/2012
Tema: 1

Thread del foro

Imagen para descargar parte 1

Imagen para descargar parte 2

Imagen para descargar parte 3

La aproximación que hacés es que como la distancia en la que vamos a averiguar el campo es mucho menor que el ancho de la placa, entonces podemos asumir que es uniforme. Con la regla de la mano derecha podemos “adivinar” el sentido que va a tener el campo, eso se muestra en el gráfico de arriba a la derecha.

Para averiguar la magnitud del campo planteamos la ley de Ampere, eligiendo la curva cuadrada C, de lado L como se muestra a la derecha inferior y queda:

La parte de la izquierda es fácil, si llamamos al campo y argumentamos por razones de simetría que es igual en la parte inferior a la placa que la superior, entonces queda , ya que en los lados de la curva C (donde el diferencial es ) el campo H y el diferencial de longitud son perpendiculares. Por otro lado, la corriente concatenada por la espira es simplemente el ancho de la espira multiplicado por la densidad. Recordemos que la densidad de corriente que se daba era lineal, ya que el espesor de la placa (el ancho en z) era despreciable. Caso contrario, tendríamos que multiplicar por la superficie y la densidad de corriente superficial. Numéricamente, 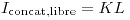. Reemplazando todo en la expresión original de la Ley de Ampere, queda:

Las se cancelan y reemplazando la relación constitutiva porque estamos en el vació llegamos a que en el punto de interés (para ),

Después pedía averiguar la inductancia mutua en la posición inicial. Para eso calculabamos el flujo concatenado y lo dividíamos por la corriente total, ie:

Para el último punto lo único que había que darse cuenta era que el flujo por definición es:

El coseno aparece de desarrollar el producto escalar de la integral de superficie. Conocida el área, la frecuencia y el campo, es cuestión de derivar el flujo con respecto al tiempo. No olvidarse de multiplicar por N para calcular el flujo total y no de una sola espira. El resultado final en magnitud es:

Donde en todos lados tenemos que reemplazar con el B que averiguamos en la primera parte.

Era fácil, salía todo haciendo los terribles choclazos de cuentas de Fourier y Newton. La unica condicion que tenías era que la temperatura de la madera no podía superar los 50°C.

Todos los circuitos llegaban al maximo de corriente en la misma frecuencia, es decir que tenían la misma frecuencia de resonancia. Como la frecuencia de resonancia depende unicamente de L y C, entonces solo se podía variar R. La respuesta correcta era que la corriente es mayor cuando el R es menor.

Se detenía mas lento el que tenía menos posibilidades (menos caminos) de generar corrientes parasíticas. Era idem al TP de inducción.

Era parecido al TP de balanza. Te pedía averiguar el B conocida la fuerza que se hacía sobre el iman y conocida la corriente + longitud de cable. Esquemáticamente:

De la balanza sacabas la fuerza sobre el imán. Por la tercera ley de Newton, la fuerza sobre el imán es igual y contraria a la fuerza sobre la espira y la fuerza sobre la espira se saca haciendo . Despejando todo eso con los datos que nos daban llegabas a:

Usando la relación de transformador ideal:

Donde p=primario y s=secundario, despejabas el numero de vueltas y de ahí aproximabas el que mas cerca estuviese, creo que era S y Q en el tema 1.

Como la corriente atrasaba la tensión, significa que el ángulo de Z es positivo. Como la parte imaginaria está dada por , significa que . Vamos opción por opción:

- Si aumento L, aumenta mas el desfasaje en vez de reducirse porque - Si aumento C, aumenta mas el desfasaje porque

Por lo tanto la única opción es jugar con la frecuencia. Además como siempre se puede ajustar la frecuencia para encontrar la resonancia, podíamos descartar las dos primeras opciones de entrada ya que una sola es la correcta. La única manera en este caso era disminuyendo la frecuencia, entonces baja y 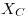sube, hasta que se hacen 0.

La lógica es la siguiente: en un imán permanente la circulación de H es 0 porque no hay corrientes libres. Además, en el vacío, B y H son paralelos. Por lo tanto, como B no cambia de sentido, H y B deben tener sentido opuesto dentro del material y paralelos en el entrehierro. La correcta era la primera.