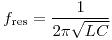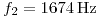Examen Parcial - 62.03./62.04. Física II - 03/12/2011
Cátedra: Para todas las cátedras
Fecha: 1º Oportunidad - 2º Cuatrimestre 2010
Día: 03/12/2011
Tema: 2
Enunciado
Problema 1
Se desea establecer en el entrehierro del núcleo de la figura un flujo de campo de inducción megnética ΦB = 2·10-5Wb. El núcelo está construido con un material de permeabilidad magnética relativa constante e igual a 600, y tiene sección transversal constante de 5 cm2, espesor e = 1mm, a = 30cm, b = 20cm. Calcular el valor y el sentido de la corriente I2 que debe circular por N2 = 1000 espiras, si la corriente I1 = 1,5 A y N1 = 400 espiras.
Problema 2
Una espira rectangular se coloca a una distancia a de un cable infinito por el que circula una corriente I = cte y en forma coplanar al cable.
| a) | Determinar el coeficiente de inducción mutua. |
| b) | Si en t = 0, la espira comienza a alejarse del cable infinito a una velocidad constante v, en la dirección perpendicular al cable, calcular la fem inducida en función del tiempo. Indicar el sentido de la corriente inducida en la espira |
| c) | Idem b), solo que la espira se desplaza paralela al cable. |
| d) | Si se hace variar la corriente que circula por el cable con el tiempo de manera que I(t) = Bt-A, con A y B constantes, ¿se modifican los resultados obtenidos en b) y c)? ¿En este caso la fem inducida es igual a la circulación de v × B a lo largo del circuito determinado por la espira? |
Problema 3
Un circuito RLC serie está excitado por un generador 12V eficaces y frecuencia f variable. Siendo L = 10mH, cuando f1 = 1592 Hz la corriente está en fase con la tensión y cuando f2 = 1674Hz la corriente atrasa 45º con respecto a la tensión.
| a) | Calcular el valor de C y R. |
| b) | ¿A que frecuencia f3 la corriente adelanta a la tensión en 45º? |
| c) | ¿Qué potencia disipa el circuito en este último caso? |
Problema 4
Describir, justificando, dos métodos para medir la frecuencia de resonancia de un circuito RLC serie con los elementos disponibles en el TP de laboratorio.
Problema 5 (SÓLO FÍSICA 2 A)
Se tiene una cañería de Hierro de 14cm de diámetro interior y 15cm de diámetro exterior, revestida con una capa de un material (de conductividad térmica λM) de 3cm, por la que circula agua a 75ºC. La temperatura exterior es 27ºC. Calcule el flujo de calor por unidad de longitud, las temperaturas de cada una de las paredes y haga un esquema de la temperatura en función del radio.
Datos: 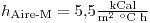 ,
,  ,
,  ,
, 
Problema 5 (SÓLO FÍSICA 2 B)
Se tiene un circuito de una malla formado por un capacitor C y una resistencia R. El capacitor se encuentra inicialmente cargado con Q0. A t = 0 se cierra el circuito. Calcule la energía disipada en la resistencia para t ≫ τ. Interprete.
Resolución
Problema 1
En el entrehierro,  y por lo tanto
y por lo tanto 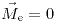 .
.
El flujo y la inducción magnética es uniforme por todo el núcleo. Para calcular 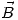 , puedo usar el flujo y la sección:
, puedo usar el flujo y la sección:

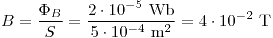
Con esto puedo calcular 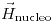 y
y 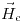 :
:



Para calcular  , puedo usar la siguiente ecuación:
, puedo usar la siguiente ecuación:
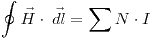

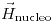 y
y  son uniformes y por lo tanto se pueden despejar:
son uniformes y por lo tanto se pueden despejar:

Despejando  , queda:
, queda:

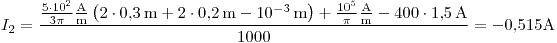
Finalmente, se toma el módulo:

Para conocer el sentido, se puede usar la ley de Faraday-Lenz, que dice que la corriente se va a dar de tal forma que estabilice el flujo, o sea, en dirección contraria a la fem.
Problema 3
Punto a
 , donde
, donde 

Cuando  , la corriente está en fase con la tensión y por lo tanto
, la corriente está en fase con la tensión y por lo tanto  (
( es la frecuencia de resonancia). Para
es la frecuencia de resonancia). Para  .
.
Diagrama fasorial:
Usando el teorema de la tangente:

En el primer caso: 
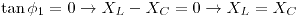
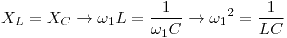
Utilizando  :
:

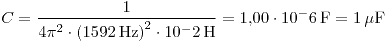
Para el segundo caso: 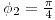
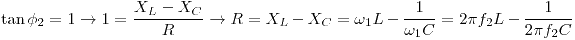
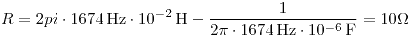
Punto b
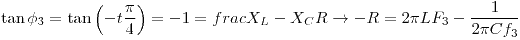
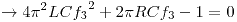
Resolviendo la cuadrática, se obtienen dos resultados:
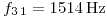

Como la frecuencia es positiva, la solución que queda es:

Punto c
Potencia aparente: 
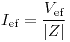
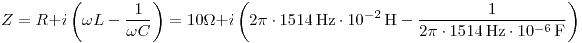
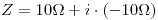


Potencia activa: 
Potencia reactiva: 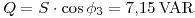
Problema 4
El primer método para medir la frecuencia de resonancia consiste en variar la frecuencia hasta que la pantalla, que debe mostrar las dos ondas y configurada de tal forma que las dos ondas tengan el mismo Vol/Div, muestre a las dos ondas como una sola.
Luego se mide la cantidad de divisiones que ocupa la onda hasta llegar a un punto con la misma altura y tangente que el punto que cruza el eje central:
A esta medida se la multiplica por el Tiempo/Div para obtener el periodo.
Finalmente, se calcula la frecuencia como la inversa del periodo.

Otra forma de hacerlo es midiendo la auto-inductancia del inductor y la capacidad del capacitor y calcular la frecuencia con la siguiente fórmula: