Examen Parcial - 62.03/04 Física II A/B
Cátedra: Santiago
Fecha: 2ª Oportunidad - 1º Cuatrimestre 2006
Día: 14/07/2006
Enunciado
Punto I
Se tiene un esfera conductora de radio  cargada con una cantidad de carga
cargada con una cantidad de carga  . Por fuera de esta esfera, se encuentra una cáscara esférica conductora de radio interior
. Por fuera de esta esfera, se encuentra una cáscara esférica conductora de radio interior  y exterior
y exterior  cargada con una cantidad de carga
cargada con una cantidad de carga  . En un momento determinado, se cierra la llave
. En un momento determinado, se cierra la llave  . Se pide:
. Se pide:
- El campo eléctrico y el potencial en todo el espacio.
- Calcular las densidades de carga.
Punto II
Encontrar la fuerza sobre la espira que transporta una corriente  , debido a un cable muy largo paralelo a la espira que transporta una corriente
, debido a un cable muy largo paralelo a la espira que transporta una corriente  .
.
Punto III
Para el circuito de la figura, determinar:
- Las corrientes en cada rama
- La carga y la energía almacenada en el capacitor
- La potencia consumida por las resistencias y la entregada y/o recibida por las pilas, indicando cuáles son generadores y cuáles receptoras.
Punto IV
(no lo copié ni tampoco me lo acuerdo… disculpas… si alguien lo tiene por favor transcríbalo)
Resolución
Punto I
!Atención: Punto I en corrección! (El procedimiento será corregido)
Cuando se conecta la llave, va haber un movimiento de cargas hacia y desde la tierra a la bola cargada. El conductor 2 está aislado.
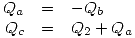
Las dendidades son :

Cálculo de E:
Para r < a :
E = 0
Dentro de un conductor el campo es cero.
Para a< r < b:
Aplicando el teorema de Gauss: 

Entonces:
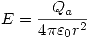
Para b< r < c:
E = 0
Dentro de un conductor el campo es cero.
Para r > c :
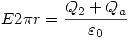
Entonces:
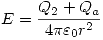
Teniendo estas expresiones en funcion de la carga en la superficie a y sabiendo que el potencial y a es cero, ya que está conectado a tierra. Entonces:
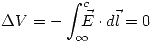
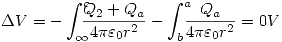

!Atención: Punto I en corrección! (El procedimiento será corregido)
Cálculo de POTENCIAL:
Para r > c :
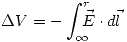


Para b< r < c:
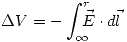


Para a< r < b:
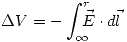


Para r < a :
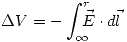
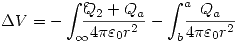

!Atención: Punto I en corrección! (El procedimiento será corregido)




