Examen Parcial - 62.03. Física II
- Enunciado
  - Punto I
  - Punto II
  - Punto III
  - Punto IV
  - Punto V
  - Punto VI
- Resolución
  - Punto I
  - Punto II
  - Punto III
  - Punto V
  - Punto VI
- Discusión

Examen Parcial - 62.03. Física II

Cátedra: Matteo-Marcet
Fecha: Segunda Oportunidad - Primer Cuatrimestre 2006
Día: 08/07/2006

Un conductor cilíndrico, recto, de radio 2 mm y longitud 1 metro se recubre con una capa de resina dieléctrica de permitividad relativa 3 y de 2mm de espesor uniforme, todo lo cual se rodea de un tubo conductor y concéntrico de radios interno 5mm y externo 6mm respectivamente. El espacio comprendido entre la resina y la superficie interna del tubo es vacío. Se aplica entre los conductores una d.d.p. de 1000 Voltios, según se ilustra en el esquema. Calcular:

La capacidad entre las superficies de radios 2 y 5 mm.
Valor y signo de las densidades de carga superficial de polarización en la resina dieléctrica.
La diferencia de potencial entre las superficies del dieléctrico correspondiente a los radios de 2 y 4 mm.
Explicar y justificar si la superficie extrena de radio 6 mm se halla cargada o no, y de qué signo sería tal carga.

Punto II

Un aro de radio 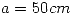$<tex>a=50cm</tex>$ tiene una carga uniforme distribuída de 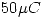$<tex>50\mu C</tex>$ . El hilo recto infinito mostrado posee una densidad de carga de 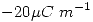$<tex>-20\mu C\ m^{-1}</tex>$ . Se pide la expresión del vector campo eléctrico resultante para todos los puntos del eje Z y el trabajo de la fuerza exterior que lleve una carga puntual de 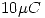$<tex>10\mu C</tex>$ , partiendo del punto 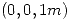$<tex>(0,0,1m)</tex>$ hasta $<tex>(0,0,2m)</tex>$ .

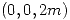Punto III

Para el circuito de c.c. calcule las potencias en valor y signo que corresponde a cada f.e.m. Calcule la carga, la polaridad del capacitor y su energía.

Punto IV

En relación al T.P. de variación de la resistencia con la temperatura, describa las manipulaciones y medidas que se efectuaron, y justifique cómo llega a evaluar el coeficiente de variación de la resistencia con la temperatura. Defina previamente dicho coeficiente, indique cuál es su unidad de medida.

Punto V

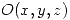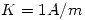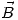Sea una terna $<tex>O(x,y,z)</tex>$ . Se tiene una corriente de superficie en todo el plano $<tex>xy</tex>$ de valor $<tex>K=1 A/m</tex>$ que corre paralela al eje $<tex>X</tex>$ en su sentido positivo. Calcule el vector $<tex>\vec{B}</tex>$ en el punto 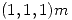$<tex>(1,1,1)m</tex>$ , y la aceleración de un protón pasante por ese punto y velocidad 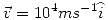$<tex>\vec v=10^4 ms^{-1} \widehat{i}</tex>$ . Masa del protón $<tex>=1.67\cdot 10^{-27}Kg</tex>$ Carga $<tex>=1.6\cdot 10^{-19} C</tex>$ .

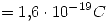Punto VI

El esquem muestro un circuito magnético de sección uniforme 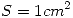$<tex>S=1 cm^2</tex>$ construído con Hipernik y Permalloy contando con un entrehierro de 1mm. Calcule la corriente que produce 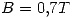$<tex>B=0.7T</tex>$ en el entrehierro, y la energía magnética así almacenada por este dispositivo.

Resolución

Punto I

Aplicando el teorema de Gauss: 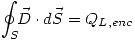$<tex>\oint_S \!\! \vec{D}\cdot d\vec{S}=Q_{L,enc}</tex>$ a una superficie cilíndrica de radio 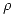$<tex>\rho</tex>$ y sabiendo que $<tex>\vec{D}(\vec{r})=D(\rho)\widehat{\rho}</tex>$ :

$<tex>D2\pi\rho h=Q_{L,enc}(\rho)</tex>$

$<tex>Q_{L,enc}(\rho)=\left\{ \begin{array}{ll}0 & 0< \rho < a \\Q_1 & a< \rho <c \\Q_1+Q_2 & c< \rho <d \\Q_1+Q_2+Q_3 & p< \rho \end{array}\right.</tex>$

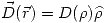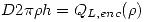
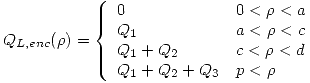
Haciendo 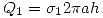$<tex>Q_1=\sigma_1 2\pi a h</tex>$

$<tex>D(\rho)=\left\{ \begin{array}{ll}0 & 0< \rho < a \\\frac{a}{\rho}\sigma_1 & a< \rho <c \\0 & c< \rho <d \\\frac{d}{\rho}\sigma_3 & p< \rho \end{array}\right.</tex>$

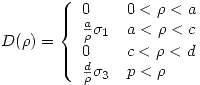
Entonces: $<tex>\begin{array}{rcl}Q_1 & = & -Q_2 \\\sigma_1 2\pi ah= -\sigma_2 2\pi ch \\\sigma_1 a = -\sigma_2 c \end{array}</tex>$

$<tex>E(\rho)=\left\{ \begin{array}{ll}0 & 0<\rho < a \\\frac{a\sigma_1}{\rho\varepsilon} & a< \rho <b \\\frac{a\sigma_1}{\rho\varepsilon_0} & a< \rho <c \\0 & c< \rho <d \\\frac{d\sigma_2}{\rho\varepsilon_0} & p< \rho \end{array}\right.</tex>$

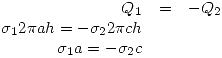
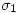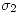Debo hallar $<tex>\sigma_1</tex>$ y $<tex>\sigma_2</tex>$ . Tengo 2 condiciones:

$<tex>\left\{ \begin{array}{rcl}\displaystyle \int_a^c \!\!\!\! \vec{E}\cdot d\vec{l} & = & -1000 V \\\displaystyle \int_d^{\infty} \!\!\!\! \vec{E}\cdot d\vec{l} & = & 1000 V \end{array}\right.</tex>$

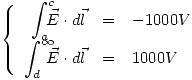
De la primera condición obtenemos:

$<tex>\begin{array}{rcl}\displaystyle\frac{a\sigma_1}{\varepsilon_r\varepsilon_0}\ln{\frac{b}{c}} + \frac{a\sigma_1}{\varepsilon_0}\ln{\frac{c}{a}} & = & -V_0 \\\displaystyle\frac{a\sigma_1}{\varepsilon_0}\ln{\frac{b^{\varepsilon_r}c}{a^{\varepsilon_r+1}}} & = & -V_0 \\\sigma_1 & = & \displaystyle -\frac{V_0\varepsilon_0}{a}\ln{\frac{a^{\varepsilon_r+1}}{b^{\varepsilon_r}c}}\\\sigma_1 & = & 13.256 \cdot 10^{-6} Cm^{-1}\end{array}</tex>$

$<tex>Q_2=-Q_1=V_0\varepsilon_0 2\pi L\ln{\frac{a^{\varepsilon_r+1}}{b^{\varepsilon_r}c}}</tex>$

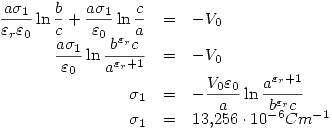
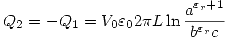
De la segunda condición obtenemos:

$<tex>\lim_{x\rightarrow \infty} \frac{a\sigma_3}{\varepsilon_0} \ln{\frac{x}{d}}=V_0</tex>$

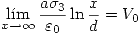
Pero la única forma de que este límite de acotado es haciendo que 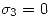$<tex>\sigma_3=0</tex>$

Para hallar la capacidad entre los conductores:

$<tex>C=\frac{Q_2}{V_0}=2\pi L\varepsilon_0 \ln{\left(\frac{a^{\varepsilon_r+1}}{cb^{\varepsilon_r}} \right)}=55.61pF</tex>$

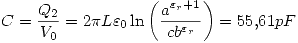
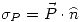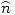Para hallar las densidades de carga de polarización usamos la fórmula que dice que en el borde de un dieléctrico $<tex>\sigma_P=\vec{P}\cdot \widehat{n}</tex>$ donde $<tex>\widehat{n}</tex>$ es la normal que apunta hacia afuera del dieléctrico.

Vemos que: 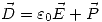$<tex>\vec{D}=\varepsilon_0\vec{E}+\vec{P}</tex>$ por considerarlo un material lineal, entonces: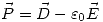 $<tex>\vec{P}=\vec{D}-\varepsilon_0\vec{E}</tex>$

Adentro del dieléctrico, es decir 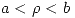$<tex>a < \rho < b</tex>$ se cumple: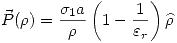 $<tex>\vec{P}(\rho)=\frac{\sigma_1 a}{\rho}\left( 1-\frac{1}{\varepsilon_r}\right)\widehat{\rho}</tex>$

Entonces en la cara $<tex>a</tex>$ y la cara $<tex>b</tex>$ del dieléctrico:

$<tex>\sigma_{P1}=\vec{P}(a)\cdot (-\widehat{\rho})=\sigma_1\left( \frac{1}{\varepsilon_r}-1 \right)=-8.837\mu Cm^{-1}</tex>$

$<tex>\sigma_{P2}=\vec{P}(b)\cdot \widehat{\rho}=\frac{a\sigma_1}{b}\left( 1-\frac{1}{\varepsilon_r}\right)=4.4187\mu Cm^{-1}</tex>$

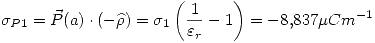
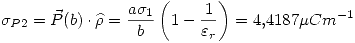
Para hallar la diferencia de potencial del dieléctrico:

$<tex>\Delta V=-\int_a^b \!\!\!\! \vec{E}\cdot d\vec{l}=-\int_a^b \!\!\!\! \frac{a\sigma_1}{\rho\varepsilon} d \rho=-\frac{a\sigma_1}{\varepsilon} \ln{\frac{b}{a}}=-692.16 V</tex>$

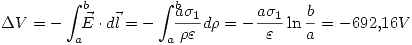
La parte de la densidad de cargas exterior fue explicada antes.

Punto II

Como el anillo tiene densidad uniforme de cargas tendríamos:

$<tex>\lambda_1=\frac{Q}{L}=\frac{50\mu C}{2\pi\cdot 0.5m}=15.9\frac{\mu C}{m}</tex>$

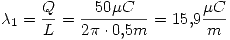
Aplicando la ley de Coulomb

$<tex>\vec{E}_1=\frac{\mu_0}{4\pi\varepsilon_0}\int \frac{\lambda_1 dl' (\vec{r}-\vec{r}')}{|\vec{r}-\vec{r}'|^3} </tex>$

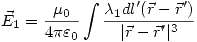
Aquí reemplazaremos lo que conocemos (calculando solo para el eje z):

$<tex>dl'=ad\varphi' \quad 0<\varphi'<2\pi \\\vec{r}=z\widehat{z} \\\vec{r}=a\widehat{\rho'}=a\cos{\varphi'}\widehat{x}+a\mathrm{sen}\varphi'\widehat{y}</tex>$

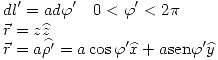
Entonces:

$<tex>\vec{E}_1=\frac{a\lambda_1}{4\pi\varepsilon_0}\int_0^{2\pi} \!\!\!\! \frac{\left( z\widehat{z}-a\cos{\varphi'}\widehat{x} -a\mathrm{sen}\varphi'\widehat{y} \right) d\varphi'}{\left( z^2+a^2 \right)^{3/2}}=\frac{a\lambda_1}{4\pi\varepsilon_0 \left( z^2+a^2 \right)^{3/2}}\left[ \widehat{z}\underbrace{\int_0^{2\pi} \!\!\!\! zd\varphi'}_{2z\pi} - \widehat{y}\underbrace{ \int_0^{2\pi} \!\!\!\! a\mathrm{sen}\varphi'd\varphi'}_{0} -\widehat{x}\underbrace{ \int_0^{2\pi} \!\!\!\! a\cos{\varphi'}d\varphi'}_{0}\right]</tex>$

$<tex>\vec{E}_1(z)=\frac{a\lambda_1}{2\varepsilon_0}\cdot\frac{z}{\left( z^2+a^2 \right)^{3/2}}\widehat{z}</tex>$

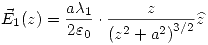
Ahora debemos encontrar el campo generado por el hilo infinito como si estuviese solo, recordando que sólo debemos hallarlo en el eje z para calcular el trabajo. Entonces si elegimos una superficie gaussiana cilíndrica de altura z, podemos suponer que el campo, por simetría, es constante en toda la superficie, y será el campo sobre el eje z a una altura z, que llamaremos 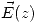$<tex>\vec{E}(z)</tex>$ . Recordamos entonces que la ley de Gauss dice: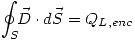 $<tex>\oint_S \!\! \vec{D}\cdot d\vec{S}=Q_{L,enc}</tex>$

Entonces: $<tex>\oint_S \!\! \vec{D}\cdot d\vec{S}=D(z)\cdot\underbrace{2\pi zh}_{\mbox{\'Area lateral}} \Rightarrow \vec{E_2}(z)=\frac{\lambda_2}{2\pi z\varepsilon_0}\widehat{z}</tex>$

Ahora aplicaremos el principio de superposición, pues supondremos que los campos generados por cada uno no son afectados por la presencia del otro.

$<tex>\vec{E}(z)=\left( \frac{a\lambda_1 z}{2\varepsilon_0\left( z^2+a^2 \right)^{3/2}} + \frac{\lambda_2}{2\pi z\varepsilon_0} \right) \widehat{z}</tex>$

Ahora sabiendo que la fuerza de oposición debe ser contraria a la fuerza eléctrica: 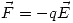$<tex>\vec{F}=-q\vec{E}</tex>$ . Por lo tanto el trabajo que debe realizarse será:

$<tex>W=\int_A^B \!\!\!\! \vec{F}\cdot d\vec{l}=-q\int_A^B \!\!\!\! \vec{E}\cdot d\vec{l}</tex>$

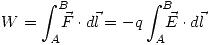
Ahora sabiendo que el trabajo este no depende del camino, elegiremos un camino por el eje z, es decir: $<tex>d\vec{l}=dz\widehat{z}</tex>$

$<tex>W=-q\int_{z_A}^{z_B} \!\!\!\! Edz= -q \left[ \frac{a\lambda_1}{2\varepsilon_0} \int_{z_A}^{z_B} \!\!\!\! \frac{z\widehat{z}}{\left( z^2+a^2 \right)^{3/2}} +\frac{\lambda_2}{2\pi\varepsilon_0} \int_{z_A}^{z_B} \!\!\!\! \frac{dz}{z} \right]</tex>$

$<tex>W=-\frac{q}{2\varepsilon_0} \left[ a\lambda_1 \left( \frac{1}{\sqrt{z_A^2+a^2}} - \frac{1}{\sqrt{z_B^2+a^2}} \right) +\frac{\lambda_2}{\pi} \ln{\frac{z_B}{z_A}} \right]</tex>$

Reemplazando por los datos que conocemos:

$<tex>W=0.6546 J</tex>$

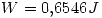
Punto III

Las corrientes están marcadas en rojo y los nodos están marcados en azul.

Aplicando las leyes de kirchof a los nodos obtenemos:

$<tex>\begin{array}{rcl}I_3+I_4 & = & I_2 \\I_1+I_2 & = & 0 \\I_4+I_5+I_6 & = & I_7 \end{array} </tex>$

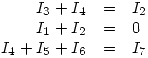
El nodo de arriba se ha evitado por obtenerse de él una ecuación linealmente dependiente con las anteriores.

Recorriendo la primer malla:

$<tex>\begin{array}{rcl}100V & = & 100\Omega I_1 - 50\Omega I_2 \\100V & = & 150\Omega I_1 \\I_1 & = & 0.667 A \\I_2 & = & -0.667 A \end{array}</tex>$

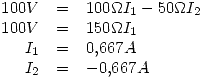
Recorriendo otra malla:

$<tex>\begin{array}{rcl}-50 V + 100 V & = & -300\Omega I_5 \\50 V & = & -300 \Omega I_5 \\I_5 & = & -0.1667 A \end{array}</tex>$

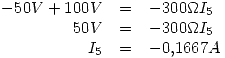
Además:

$<tex>50V = -200 \Omega I_6 \quad \Rightarrow \quad I_6=-0.25A</tex>$

$<tex>50 V = 300 \Omega I_7 \quad \Rightarrow \quad I_7=0.1667A</tex>$

$<tex>I_4=I_7-I_5-I_6 \quad \Rightarrow \quad I_4=0.583A</tex>$

$<tex>I_3=I_2-I_4 \quad \Rightarrow \quad I_3=-1.25A</tex>$

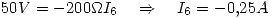
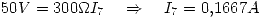
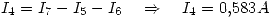
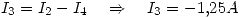
Por como se eligieron las corrientes (sabiendo que para calcular la potencia se toma la diferencia de tensión en el sentido de la corriente):

$<tex>\begin{array}{rccclcl}P_{3} & = & I_3 E_3 & = & -125 W & \quad \quad & \mbox{consumida} \\P_{4} & = & I_4 E_4 & = & 29.167 W & \quad \quad & \mbox{entregada} \end{array}</tex>$

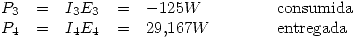
Para hallar la carga del capacitor vemos que la diferencia de potencial del capacitor es 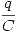$<tex>\frac{q}{C}</tex>$ , entonces:

$<tex>\frac{q}{C}=50\Omega (-0.667A)+50V=16.65V</tex>$

$<tex>q=1665\mu C</tex>$

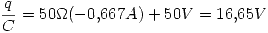
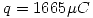
Como la carga dio positiva yendo de izquierda a derecha, entonces la polaridad del capacitor es: + a la derecha y - a la izquierda según el diagrama.

La energía almacenada en el capacitor:

$<tex>U_C=\frac{1}{2} C(\Delta V)^2=13.86mJ</tex>$

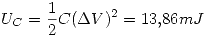
Punto V

El esquema del problema es el siguiente:

Este ejercicio puede resolverse de dos formas: Ley de Ampère o Ley de Biot-Savart

La ley de Ampère requiere una justificación excesiva de parte de este ejercicio, y además se necesita conocer el sentido del campo antes de aplicarla, por lo cual aplicare la ley de Biot-Savart.

En este caso esta ley se escribe como: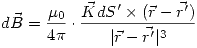 $<tex>d\vec{B}=\frac{\mu_0}{4\pi}\cdot\frac{\vec{K}dS'\times (\vec{r}-\vec{r'})} {|\vec{r}-\vec{r'}|^3}</tex>$

En este caso tenemos los siguientes datos:

$<tex>dS'=dx'dy'\\\vec{K}=K\widehat{x} \\\vec{r}=z\widehat{z} \\\vec{r'}=x'\widehat{x}+y'\widehat{y} </tex>$

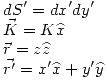
Entonces (además sabemos que el plano es infinito):

$<tex>\vec{B}=\frac{\mu_0 K}{4\pi} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \!\!\!\! \frac{\widehat{x} \times \left( -x'\widehat{x}-y'\widehat{y}+z\widehat{z} \right)}{ \left[ {x'}^2+{y'}^2+z^2 \right]^{3/2}}dx'dy'</tex>$

$<tex>\vec{B}=\frac{\mu_0 K}{4\pi} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \!\!\!\! \frac{ -y'\widehat{z} -z\widehat{y}}{ \left[ {x'}^2+{y'}^2+z^2 \right]^{3/2}}dx'dy'</tex>$

Separando el campo en sus componentes:

$<tex>B_x= - \frac{\mu_0 K}{4\pi} \int_{-\infty}^{\infty} \!\!\!\! dx' \int_{-\infty}^{\infty} \!\!\!\! \frac{y'dy'}{\left[ {x'}^2+{y'}^2+z^2 \right]^{3/2}}dx'dy'=0 \quad \mbox{pues es una funci\'on impar}</tex>$

$<tex>B_y= \frac{\mu_0 K}{4\pi} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \!\!\!\! \frac{-zdx'dy'}{\left[ {x'}^2+{y'}^2+z^2 \right]^{3/2}}=-\frac{\mu_0 Kz}{4\pi} \int_{-\infty}^{\infty} \!\!\!\! dx' \left( \frac{2}{{x'}^2+z^2} \right)</tex>$

Esto es:

$<tex>B_y=-\frac{\mu_0 Kz}{2\pi} \int_{-\infty}^{\infty} \!\!\!\! \left( \frac{dx'}{{x'}^2+z^2} \right)= -\frac{\mu_0 Kz}{2\pi} \left[ \left. \frac{1}{|z|} \mathrm{arctg} \left( \frac{x'}{z} \right) \right|_{-\infty}^{\infty} \right]</tex>$

Recordando el comportamiento de la función arcotangente:

Y además sabiendo que la función 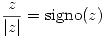$<tex>\frac{z}{|z|}=\mathrm{signo}(z)</tex>$ , entonces:

$<tex>B_y=-\frac{\mu_0 K}{2\pi} \left[ \frac{\pi}{2} - \left( - \frac{\pi}{2} \right) \right] \mathrm{signo}(z)</tex>$

$<tex>\vec{B}=\frac{\mu_0 K}{2}\mathrm{signo}(z)\widehat{y}</tex>$

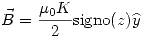
Que es lo que debíamos hallar. Reemplazando los datos numéricos:

$<tex>\vec{B}=\left\{ \begin{array}{lcl}6.283\cdot 10^{-7} T & \quad & z>0 \\-6.283\cdot 10^{-7} T & \quad & z<0 \end{array} \right.</tex>$

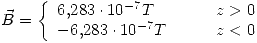
Ahora vamos a hallar la aceleración del protón.

En el punto P 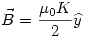$<tex>\vec{B}=\frac{\mu_0 K}{2}\widehat{y}</tex>$

Sabiendo que la fuerza de Lorentz debifa a un campo magnético es: 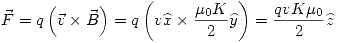$<tex>\vec{F}=q\left( \vec{v} \times \vec{B} \right) = q\left( v\widehat{x} \times \frac{\mu_0 K}{2} \widehat{y} \right)=\frac{qvK\mu_0}{2}\widehat{z}</tex>$

Usando la ley de Newton: 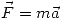$<tex>\vec{F}=m\vec{a}</tex>$

$<tex>\vec{a}=\frac{qvK\mu_0}{2m}\widehat{z}</tex>$

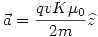
Reemplazando los datos numéricos: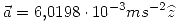 $<tex>\vec{a}=6.0198\cdot 10^{-3} ms^{-2} \widehat{z}</tex>$

Punto VI

Si aplicamos la ley de Ampère al material de la figura, haciendo las consideraciones necesarias obtenemos:

$<tex>\oint_{\mathcal{C}} \vec{H}\cdot\vec{dl} = I_{conc}</tex>$

$<tex>H_PL_P+H_HL_H+H_eL_e = NI</tex>$

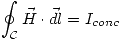
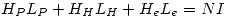
Donde los subíndices se refieren a Permalloy, Hipernick y entrehierro respectivamente.

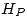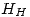Si el material está inicialmente desmagnetizado entonces debo hallar en la tabla los valores de $<tex>H_P</tex>$ y $<tex>H_H</tex>$ que den un $<tex>B=0.7T</tex>$ .

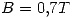La tabla dice:

$<tex>\begin{array}{c|c|c}H(Am^{-1}) & B(T) \mbox{Permalloy} & B(T) \mbox{Hipernick} \\\hline7.2 & 0.700 & 0.440 \\\vdots & \vdots & \vdots \\16.0 & & 0.650 \\24.0 & & 0.765 \end{array}</tex>$

De la tabla sale que 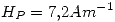$<tex>H_P=7.2 Am^{-1}</tex>$ ; y además interpolando linealmente entre los valores de Hipernik aproximamos $<tex>H_H=19.8095 Am^{-1}</tex>$

También sabemos que 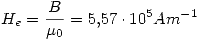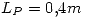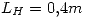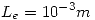$<tex>H_e=\frac{B}{\mu_0}=5.57\cdot 10^5 Am^{-1}</tex>$ , $<tex>L_P=0.4m</tex>$ , $<tex>L_H=0.4m</tex>$ , $<tex>L_e=10^{-3}m</tex>$ y $<tex>N=500</tex>$

Entonces resulta 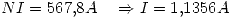$<tex>NI=567.8 A \quad \Rightarrow I=1.1356 A</tex>$

Para calcular la energía podemos calcular la autoinductancia del sistema:

$<tex>L=\frac{d\phi}{dI}=S\frac{dB}{dI}=S\frac{B}{I}=61.64\cdot 10^{-6} Hy</tex>$

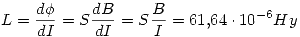
Entonces: 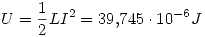$<tex>U=\frac{1}{2}LI^2=39.745\cdot 10^{-6}J</tex>$

Discusión

Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá o al mail GastonK

En la resolución del punto 1 (a), creo que no esta bien definida la superficia gaussiana. Si consideramos el largo del cilindro del problema como “infinito”, entonces ahi si podemos usar una sup. gaussiana pero de largo menor al del cilindro. Entonces si h es el largo del cilindro, diríamos que h' es el largo de la superficie gaussiana, y tener cuidado ahora porque la Q libre encerrada ahora es distinta. Por ejemplo, para un radio entre a y b daría algo como: Q(l,enc) = (Qa.2.pi.a^2.h')/ (2.pi.a^2.h) Esto no fue mas que un formalismo porque después las cuentas dan exactamente igual, pero creo que vale la pena aclarlo, si es que no lo hicieron bien.