Examen Parcial - 62.03/04 Física II A/B
Cátedra: Todas
Fecha: 1ª Oportunidad - 1º Cuatrimestre 2006
Día: 20/05/2006
Enunciado
Punto I
Para el circuito de la figura, determnar:
- Las corrientes en cada rama
- La carga y la energía almacenada en el capacitor
- La potencia consumida por las resistencias y la entregada y/o recibida por las pilas, indicando cuáles son generadores y cuáles receptoras.
Datos:
Punto II
Responder, justificando:
- ¿Es cierto que sobre un conductor en condiciones de equilibrio electrostático el potencial es constante? ¿Y el campo eléctrico?
- Al cargar un conductor que tiene forma irregular como en la figura, ¿dónde se acumulan las cargas?
- Si un conductor hueco se carga ¿cómo se distribuyen las cargas? Hacer un esquema de la distribución de cargas y del campo eléctrico sobre la superficie del conductor.
- Describa los resultados obtenidos para la distribución nube-pararrayos del Trabajo Práctico “Distribuciones de carga”.
Punto III
Una distribución lineal de carga uniforme, con carfa por unidad de longitud 
, tiene forma de arco circular de radio R como muestra la figura. El arco subtiende un ángulo de 180º.
- Determine el campo eléctrico sober un eje perpendicular a la figura que pasa por T.
- ¿Qué trabajo debe realizar una fuerza exterior para desplazar una carga puntual q desde el infinito hasta el punto T?
- Determine la fuerza que ejerce esta distribución sobre una carga puntual Q ubicada en el punto T si la configuración está en el vacío.
- Si el espacio fuera un material dieléctrico de constante dieléctrica
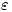, ¿sería la fuerza mayor, menor o igual que en el caso del vacío? ¿Por qué?
Punto IV
Un material magnético tiene una curva B-H que asemeja un paralelogramo cuyos vértices son:
.
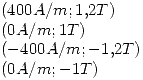Para valores de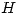 
cuyo módulo supere los 
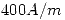se considera que el medio está saturado. Con este material se construye un toroide de sección cuadrada, radio interno 
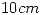y externo 
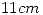. La pieza tiene un entrehiero de 
y sobre ella se bobinan 100 vueltas de alambre.
Determinar:
- La corriente necesaria para saturar el material.
- Los valores de
, 
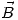y 
en el núcleo y en el entrehierro cuando se interrumpe la corriente.
Punto V
Se tienen cuatro cables paralelos de longitud 
y radio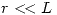 
dispuestos como indica la figura (como si fueran las aristas de un prima de base cuadrada de lado 
). Por cada uno de ellos circula una corriente I con el sentido que también se indica en la figura.
- Calcular el campo magnético en los puntos D y Q (muy alejados de los extermos).
- Hacer una descripcion (CUALITATIVA) del movimiento que realizaría una carga
que pasara con velocidad 
por el punto D como indica la figura.
Resolución
Punto I
[el esquema me falta escanearlo]
Parte 1
Como en una de las corrientes conectadas a tierra hay un capacitor, entonces, en régimen estacionario no circulará corriente por ninguna de ambas ramas.
Las ecuaciones de mallas dicen:
De la primera despejamos:
De la segunda:
Entonces la ecuación de nodos dice: 
Por lo tanto 
Es decir que los sentidos de las corrientes están alrevés.
Parte 2
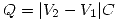y el signo de 
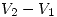me dará la polaridad.
Por lo que: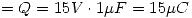 
.
Y por lo tanto la carga positiva está “en el lado contrario a la tierra”.
Parte 3
La potencia consumida en las ersistencias se calcula:
La potencia en las fuentes se cálcula con la corriente en el sentido de la fem y luego el signo me dice si es recibida o entregada.
Vemos que se cumple el balance de energías pues si sumamos toda la potencia entregada por las fuentes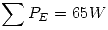 
nos da igual que la potencia consumida en las resistencias 
.
Punto II
1) En el interior de un conductor el campo es constantemente nulo, y el potencial electrostático es 
y entonces 
en todo el interior del conductor, lo que indica que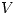 
es constante dentro del conductor.
2) Para que se mantenga el potencial constante en todo el interior del conductor las cargas deben ubicarse de manera que la densidad de cargas sea mayor en la punta más aguda (la de radio de curvatura menor).
3) Si un conductor hueco se carga las cargas se distribuyen en la cara exterior del conductor de manera que en el interior (por la ley de gauss ya que no hay carga encerrada) el campo debe ser nulo. En las proximidades del conductor el campo es perpendicular a la superficie del conductor.
4) Este mismo efecto se observa en el parrarayos, pues al ser una punta muy aguda hace que el campo eléctrico sea muy alto en el pararrayos disminuyendo el campo eléctrico de alrededor.
Punto III
Parte 1
Calculamos el campo eléctrico con la ley de Coulomb: 
En esto vamos a reemplazar los datos para este problema:
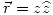
![<tex>|\vec{r}-\vec{r'}|^3=[z^2+R^2]^{3/2}</tex>](lib/plugins/latex/images/8731ae736e58ec470050fabf2ec490131b814b52_0.png "<tex>|\vec{r}-\vec{r'}|^3=[z^2+R^2]^{3/2}</tex>")
Reemplazando ahora en la fórmula de Coulomb integrada:
![<tex>\vec{E}=\frac{\lambda R}{4\pi\varepsilon_0}\int_0^{\pi}d\varphi'\frac{z\widehat{z}-R\cos{\varphi'}\widehat{x}- R\mathrm{sen}\varphi'\widehat{y}}{[z^2+R^2]^{3/2}}=\frac{\lambda R}{4\pi\varepsilon_0[z^2+R^2]^{3/2}}\left[ z\int_0^{\pi}d\varphi'\widehat{z}\ -\ R\int_0^\pi\cos{\varphi'}d\varphi'\widehat{x}\ -\ R\int_0^\pi\mathrm{sen}\varphi'd\varphi'\widehat{y}\right]</tex>](lib/plugins/latex/images/9645bfe3ab5a4e904db6b243c92afc543f454b45_0.png "<tex>\vec{E}=\frac{\lambda R}{4\pi\varepsilon_0}\int_0^{\pi}d\varphi'\frac{z\widehat{z}-R\cos{\varphi'}\widehat{x}- R\mathrm{sen}\varphi'\widehat{y}}{[z^2+R^2]^{3/2}}=\frac{\lambda R}{4\pi\varepsilon_0[z^2+R^2]^{3/2}}\left[ z\int_0^{\pi}d\varphi'\widehat{z}\ -\ R\int_0^\pi\cos{\varphi'}d\varphi'\widehat{x}\ -\ R\int_0^\pi\mathrm{sen}\varphi'd\varphi'\widehat{y}\right]</tex>")
De las tres integrales, la segunda se hace cero y la última vale 2, entonces:
![<tex>\vec{E}=\frac{\lambda R}{4\pi\varepsilon_0[z^2+R^2]^{3/2}}\left(z\pi\widehat{z}-2R\widehat{y}\right)</tex>](lib/plugins/latex/images/aa05ce545491ed9e4988b374619b9a7e6b08e0cb_0.png "<tex>\vec{E}=\frac{\lambda R}{4\pi\varepsilon_0[z^2+R^2]^{3/2}}\left(z\pi\widehat{z}-2R\widehat{y}\right)</tex>")
Parte 2
El trabajo debe calcularse con una fuerza exterior, que debe ser contraria a la ejercida por la distribución de cargas 
, y entonces 
Si elijo una trayectoria por el eje z: 
. Al hacer el producto escalar con el campo eléctrico sólo va a aportar la componente z del campo, es decir:
![<tex>W=-q\int_{-\infty}^0 E_zdz=-q\int_{-\infty}^0\frac{\lambda Rzdz}{4\pi\varepsilon_0[z^2+R^2]^{3/2}}=- \frac{q\lambda R}{4\pi\varepsilon_0}\int_{-\infty}^0 \frac{zdz}{[z^2+R^2]^{3/2}}</tex>](lib/plugins/latex/images/e44518964e5342cc2b445bf3b70657b6916ff449_0.png "<tex>W=-q\int_{-\infty}^0 E_zdz=-q\int_{-\infty}^0\frac{\lambda Rzdz}{4\pi\varepsilon_0[z^2+R^2]^{3/2}}=- \frac{q\lambda R}{4\pi\varepsilon_0}\int_{-\infty}^0 \frac{zdz}{[z^2+R^2]^{3/2}}</tex>")
Para resolver la integral buscamos la primitiva en la tabla:
![<tex>\int_{-\infty}^0 \frac{zdz}{[z^2+R^2]^{3/2}}=\left. \frac{z}{R^2\sqrt{z^2+R^2}}\right|_{-\infty}^0</tex>](lib/plugins/latex/images/f2da845c45981f28f054bd6f701abcf695217abf_0.png "<tex>\int_{-\infty}^0 \frac{zdz}{[z^2+R^2]^{3/2}}=\left. \frac{z}{R^2\sqrt{z^2+R^2}}\right|_{-\infty}^0</tex>")
CUIDADO Creo que está mal la primitiva. Debería ser esta: 
(List of integrals of irrational functions).
Todas las conclusiones siguientes pueden estar mal.
Fhran.
Efectivamete, la integral da finalmente -1/R, con lo cual W no dependería de R.
4WD
Ahora resolvemos el límite:
Entonces la integral da como resultado 
, y entonces:
Parte 3
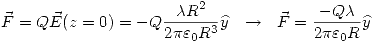
Parte 4
y como 
Punto IV
Consideraciones a tener en cuenta:
- El toroide está hecho de un material ferromagnético dado que la relación entre 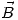y no es lineal y se relacionan de la siguiente manera: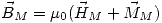
- En el entrehierro la relación entre 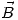y es lineal.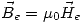
- Fuera del toroide se considera nulo el campo magnético.
- En el entrehierro las líneas de campo tenderían a abrirse pero, dado que la dimensión del entrehierro es varios órdenes de magnitud inferior al resto de las dimensiones del problema, este efecto se considera despreciable.
- Dado que el toroide posee una sección angosta la variación en dirección radial de y 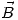se considera nula.
- Tanto como tienen dirección
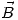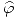
- Como
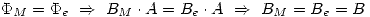
Planteamos la ley de Ampere generalizada 
Para hacer la circulación (por consideración 5) puedo considerar una circunferencia con radio medio (punteada).
Como y 
son paralelos a lo largo de la curva elegida, el producto escalar es equivalente al producto de sus módulos.
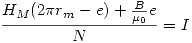
Reemplazando los valores:
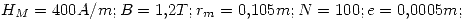
Se obtiene: 
Segunda parte
Si se interrumpe la corriente tenemos:
Como sigue valiendo , se llega a:
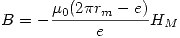
Esta ecuación nos está indicando que entre 
y 
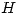hay una relación lineal, y dicha recta pasa por el origen de coordenadas. Para conocer los valores de , y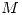 
tengo que encontrar la intersección de esta recta con la curva de histéresis.
Como estamos aproximando la curva de histéresis con un paralelogramo, podemos obtener la ecuación de la “recta de histéresis”: 
.
Igualando esta recta con la recta de la ecuación de Ampère: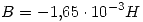 
. Obtenemos 
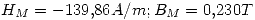. Entonces:
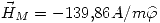
El valor de sale de la relación 
. Es decir:
En tanto que en el entrehierro, por las consideraciones realizadas en el punto 7.
.
Por supuesto que en el entrehierro: 
.
Considerando el punto 2, se obtiene que:
