Examen Parcial - 62.03./04. Física II A/B

Cátedra: Todas las cátedras
Fecha: Primera Oportunidad - Primer Cuatrimestre 2004
Día: 08/05/2004

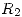Una esfera conductora de radio y carga está rodeada por una cáscara conductora de radios y descargada.

1. Calcular las densidades de carga en las superficies de la esfera y en ambas superficies de la cáscara.
2. Se coloca a continuación una batería (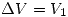) entre la esfera y la cáscara y se cierra . Calcule a continuación las densidades de carga calculadas en el punto anterior.
3. A continuación y manteniendo esta configuración se introduce un dieléctrico de permitividad relativa entre la esfera y la cáscara. Calcule 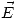, 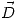y 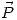en todo el espacio y las densidades de carga libre y de polarización en cada una de las superficies.
4. Se abre ahora la llave y se conecta la cáscara conductora a tierra cerrando . Calcule en este caso las densidades de carga en las superficies

Tres esferas de radios , 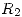y ( y ) se encuentran separadas entre si por una distancia como indica la figura. Inicialmente la esfera 2 se encuentra cargada con una carga mientras que las otras esferas están descargadas. Las llaves están todas abiertas. Se cierra primero la llave . Luego se abre y se cierra . Calcule el potencial en el punto P.

1. Calcular el valor de una resistencia utilizando el circuito de conexión larga si el amperímetro mide (en escala de ) y el voltímetro mide (en escala de ). Los instrumentos están fabricados con dos galvanómetros de y corriente máxima .
2. Se tienen dos capacitores planos idénticos y cuyas placas están separadas 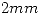y tienen un radio de . El primer capacitor, , está conectado a un electrómetro 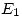que tiene una capacidad de entrada de . Se aplica, con una batería, una diferencia de potencial de entre las placas de . Luego se desconecta la batería. Al segundo capacitor también se le aplica una diferencia de potencial de y luego se lo conecta a otro electrómetro que tiene las mismas caracterísiticas que 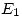. Se desconecta la batería. a) ¿Marcan los dos electrómetros el mismo valor? b) Si se separan las placas de y hasta ¿Marcan los dos electrómetros el mismo valor? Justifique en cada caso.

En el circuito de la figura, determine:

1. La corriente en cada rama
2. La carga del capacitor
3. El potencial en los puntos A,B,C y D

Se tiene un tramo de conductor de largo por el que circula una corriente en la dirección (Ver Figura). Otro conductor que puede considerarse infinito y ubicado en el plano , paralelo al eje y a una distancia transporta una corriente . Calcule la fuerza sobre un positron de cuando se encuentra justo pasando por el punto .

Datos: .

Antes que nada vamos a utilizar la Ley de Gauss, que dice que para una superficie cerrada 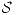del espacio se cumple siempre

Si aplicamos esto a este problema utilizando 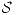como una superficie esférica concéntrica con las del problema de radio se cumple que:

Donde vamos a tomar un sistema de referencia centrado en las esferas y las variables , y son las coordenadas esféricas.

En este problema podemos suponer que la simetría esférica nos da:

Ahora si reemplazamos obtenemos:

Esta ecuación es válida en cualquiera de las partes del problema, pues no se ha supuesto ninguna consideración acerca de la configuración de las cargas.

Ahora podemos resolver la en función de . Si usaremos las cargas primadas para llamar a las cargas de las superficies de configuraciones después de la distribución:

En esta parte del problema vemos que las dos partes están aisladas y por lo tanto no transferirán cargas entre si, y podremos decir que la carga total de cada conductor es igual antes y después de la distribución:

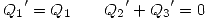
Ahora resolvemos:

Si ahora usamos la conservación de la carga:

Pero una de las propiedades de los conductores es que en su interior el campo eléctrico es nulo, por lo tanto entonces:

Usando todos estos datos sobre las cargas sobre cada superficie, podemos hallar las densidades de cargas pedidas en función de los datos del problema:

Se cierra

La ecuación sigue valiendo en este caso pero no así la ecuación de conservación anterior pues ambos conductores no están aislados entre si. Pero en cambio, sí están aislados con el resto del espacio y por lo tanto se conservará su carga total, es decir:

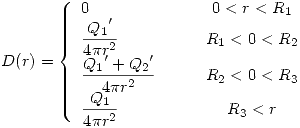
Al igual que antes de acá se desprende 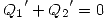y por lo tanto podemos obtener ahora el campo eléctrico en todo el espacio:

Ahora para hallar la incógnita que nos falta (que es ) usamos la condición de la diferencia de potencial entre las placas fijada por la pila:

Usamos un camino radial entonces:

Por lo tanto:

Ahora vamos a escribir las densidades de cargas libres en las superficies (considerándolas uniformes al igual que antes):

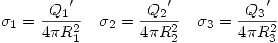
Que están en función de datos del problema.

En la figura se muestran los sentidos de las corrientes elegidos para aplicar las leyes de Kirchoff.

La ley de nodos arroja:

Circulando por dos mallas:

Escribiendo las ecuaciones en forma de sistema matricial:

La resolución del sistema da:

Para hallar la carga del capacitor usaremos el resultado que dice que la diferencia de potencial en el capacitor está dado por el cociente entre la carga y la capacidad; además usaremos que la diferencia de potencial no depende del camino. Entonces:

Como obtenemos que y por lo tanto . Con esto concluimos que la carga positiva del capacitor está en la placa cercana al punto A y la carga negativa en la cercana al punto D.

Para hallar el potencial en los puntos pedidos debo asignar antes una referencia. Por comodidad planteamos que . Esto nos servirá pues sabemos que B está conectado directamente a tierra y por lo tanto tendrá el mismo potencial que el infinito