Examen Final - 62.03. Física II A / 62.04. Física II B - 05/07/2013
Cátedra: Todas
Fecha: Primer Oportunidad - Invierno 2013
Día: 05/07/2013
Enunciado
Punto I
Sea un circuito RLC-Serie conectado a una fuente de 220V eficaz y frecuencia 50Hz. Sabiendo que 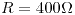 y que
y que 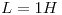 se pide:
se pide:
- Calcular
 para que el circuito tenga un comportamiento capacitivo de forma tal que el factor de potencia sea
para que el circuito tenga un comportamiento capacitivo de forma tal que el factor de potencia sea 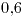 . Hacer diagrama fasorial.
. Hacer diagrama fasorial. - Para el valor de
 encontrado anteriormente: ¿Cuál es el valor de
encontrado anteriormente: ¿Cuál es el valor de  para que el circuito esté en resonancia? Hacer el diagrama fasorial para este caso.
para que el circuito esté en resonancia? Hacer el diagrama fasorial para este caso.
Punto II
- Un cuerpo cargado modelado como puntual está fijo y tiene una carga
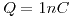 . Para mover en forma isotérmica y cuasiestacionaria una carga puntual q desde la distancia
. Para mover en forma isotérmica y cuasiestacionaria una carga puntual q desde la distancia 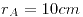 hacia una distancia
hacia una distancia 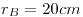 de la carga Q se necesita realizar un trabajo
de la carga Q se necesita realizar un trabajo  . Calcular el valor de la carga q.
. Calcular el valor de la carga q. - Ambas cargas se sumergen en un medio líquido con propiedades dieléctricas lineales, homogéneas e isotrópicas. Calcular el valor de la permitividad relativa para que el trabajo realizado en el punto anterior sea la mitad. Calcular
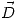 ,
,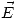 ,
,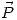 debido a un Q en punto situado 40cm de esta carga cuando el medio es el dieléctrico.
debido a un Q en punto situado 40cm de esta carga cuando el medio es el dieléctrico.
Punto III
 Un disco macizo conductor de radio
Un disco macizo conductor de radio 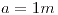 gira con velocidad angular constante en un campo magnético constante y uniforme de módulo
gira con velocidad angular constante en un campo magnético constante y uniforme de módulo 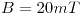 perpendicular al plano del disco como muestra la figura. En el borde y en el centro del mismo, dos “escobillas rozantes” se conectan a un resistor de resistencia
perpendicular al plano del disco como muestra la figura. En el borde y en el centro del mismo, dos “escobillas rozantes” se conectan a un resistor de resistencia 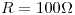 , estableciendo una corriente
, estableciendo una corriente 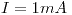 como se indica en la figura.
como se indica en la figura.
- Calcular el valor y el sentido de la velocidad angular
 del disco.
del disco. - Si conecta un inductor de autoinductancia
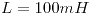 y resistencia interna
y resistencia interna 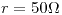 en serie con el resistor, calcular el nuevo valor de la corriente
en serie con el resistor, calcular el nuevo valor de la corriente 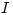 .
.
Punto IV (Física IIA y Física II)
- Describa la experiencia de Joule de la expansión libre de un gas ideal calculando la variación de la entropía del gas y las conclusiones que se obtienen.
- Determine la relación entre el calor específico a presión constante, el calor específico a volumen constante y la constante universal de los gases ideales.
Punto IV (Física II B)
- Escriba las ecuaciones de Maxwell en el vacío de forma diferencial e integral comentando brevemente cada una de ellas.
- Demuestre la expresión de la potencia instantánea para un circuito resistivo puro excitado con un generador de voltaje alterno. Grafique la potencia instantánea en función del tiempo para un período indicando la potencia activa y cuál es el significado físico de esta.
Punto V (Física IIA y Física II)
- Escriba los enuciados de Kelvin-Planck y Clausius del segundo principio de la termodinámica
- Demuestre la equivalencia de los enunciados del punto anterior.
Punto V (Física II B)
Se tiene un toroide con permeabilidad relativa  y sección cuadrada de indo
y sección cuadrada de indo 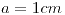 . El radio interior es
. El radio interior es 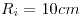 y existe un entrehierro
y existe un entrehierro 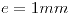 . Tiene un arrollamiento de
. Tiene un arrollamiento de  vueltas por el cual se establece una corriente de
vueltas por el cual se establece una corriente de 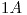 , y otro arrollamiento de
, y otro arrollamiento de 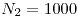 en el cual no hay corriente.
en el cual no hay corriente.
- Calcular los coeficientes de autoinducción y de inducción mutua.
- Hallar los vectores
 ,
,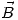 ,
, en el punto medio del entrehierro, y en cualquier punto del radio medio del toroide.
en el punto medio del entrehierro, y en cualquier punto del radio medio del toroide.
Resolución
