Examen Final - 62.03. Física II A - 02/08/2012
Cátedra: Todas
Día: 02/08/2012
En el foro:
Coloquio 02/08/12
Enunciado
Punto I
Un cable coaxial muy largo está formado por un conductor central de radio a y una malla de radios interior b y c. Por el conductor central circula una corriente I, uniformemente distribuida en la sección transversal. La misma corriente uniformemente distribuida retorna por la malla. Considere que los conductores están en vacío.
Parte a
Determinar el campo  en todo el espacio.
en todo el espacio.
Parte b
Calcular la energía almacenada por unidad de longitud, y a partir de ésta, la inductancia por unidad de longitud.
Punto II
(Transcripción no literal)
a) Explicar el significado de bornes homólogos
b) Deducir la expresión de inductancia total de dos bobinados en serie (Datos: 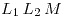 )
)
Punto III
Punto IV
(Sólo Física II A)
Un motor opera entre dos fuentes de 400°C y 100°C
Parte a
Determinar la mínima cantidad de calor que se debe entregar a la fuente fría si se desea obtener 100J de trabajo.
Parte b
Si con las mismas temperaturas y trabajo el motor tomara 500J de la fuente caliente, determinar si sería un motor irreversible,reversible o imposible.
Punto V
(Sólo Física II A)
En un calorímetro ideal, hay 2Kg de agua y 2Kg de hielo en equilibrio a presión atmosférica. Se agregan 1Kg de agua a 90°C (calor específico del agua 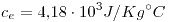 , calor latente
, calor latente  )
)
Parte a
Calcular la temperatura de equilibrio.
Parte b
Calcular el cambio de entropía del sistema y del universo.
Resolución
Punto I
Parte a
Definimos las densidades de corriente por unidad de longitud llamando  a la corriente en el conductor central y
a la corriente en el conductor central y  a la corriente en la malla, teniendo en cuenta la uniformidad mencionada en el enunciado:
a la corriente en la malla, teniendo en cuenta la uniformidad mencionada en el enunciado:

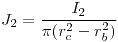
Tomamos que  dentro de un conductor es 1, por lo tanto en todo el espacio usamos la relación
dentro de un conductor es 1, por lo tanto en todo el espacio usamos la relación 
Uso la ley de Ampere para calcular el campo en todo el espacio que divido en secciones:
a)Dentro del conductor central
b)Entre la malla y el conductor
c)Dentro de la malla
d)Fuera del cable
Tomando como sistema de referencia un sistema de coordenadas cilíndrico con eje z en el centro del cable, con  yendo en sentido positivo y
yendo en sentido positivo y  en sentido opuesto, y una curva amperiana (dentro de la sección correspondiente) tal que el campo es uniforme sobre ella entonces:
en sentido opuesto, y una curva amperiana (dentro de la sección correspondiente) tal que el campo es uniforme sobre ella entonces:
a) 


b) 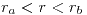

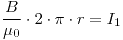
c) 


d) 

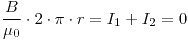
Con esto podemos despejar B en función de los datos.
Parte b
Usamos la fórmula de densidad volumétrica de energía en el campo electromagnético
 donde
donde 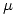 depende de
depende de 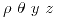 y como queremos obtener la energía por unidad de longitud integramos con respecto a las variables
y como queremos obtener la energía por unidad de longitud integramos con respecto a las variables 
 teniendo en cuenta que como el valor del campo cambia según la región, hay que separar, una integral por cada región.
teniendo en cuenta que como el valor del campo cambia según la región, hay que separar, una integral por cada región.
Luego tomamos la expresión para la energía en un inductor 
Dividimos la expresión por  para obtener la energía por unidad de longitud:
para obtener la energía por unidad de longitud:

Y obtenemos finalmente la inductancia por unidad de longitud:

Punto II
Punto III
Punto IV
Parte a
Como en una máquina térmica  por ser un proceso cíclico y U, función de estado, según el primer principio de la termodinámica |W|=|Q| donde
por ser un proceso cíclico y U, función de estado, según el primer principio de la termodinámica |W|=|Q| donde 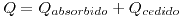 . Según nuestra convención (calor que entra al sistema es positivo, el que sale es negativo) entonces
. Según nuestra convención (calor que entra al sistema es positivo, el que sale es negativo) entonces 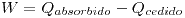 .
.
En este caso el rendimiento que calculamos como 
Podemos ver entonces que una máquina que entregue la menor cantidad de Q (condición del enunciado) será la de mayor rendimiento (teniendo  cte). Entonces según el enunciado de Carnot:
cte). Entonces según el enunciado de Carnot:
“La eficiencia de cualquier máquina térmica que opere entre dos temperaturas específicas nunca podrá superar la eficiencia de una máquina Carnot que opere entre las mismas dos temperaturas” (Resnick Tomo I, sección 26-4)
Calculamos el rendimiento de nuestro motor como el rendimiento de una máquina de Carnot entre 673°K y 373°K:
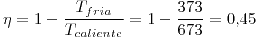 (Rendimiento del 45\%)
(Rendimiento del 45\%)
Ya que se desea obtener 100 J de trabajo:
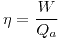
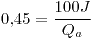

De 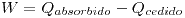
Respondemos: 
Parte b
El carácter reversible o no se puede analizar mediante la desigualdad de Clausius para un sistema:

donde la igualdad se cumple en caso de tratarse de un sistema reversible y la desigualdad en caso de tratarse de un sistema irreversible. En otro caso, la máquina es imposible.
Calculamos el nuevo Q cedido para esta situación:



En la desigualdad de Clausius, donde el calor cedido al medio es negativo por convención:
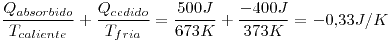
Respuesta: Sería un motor irreversible
Punto V
Parte a
Calorímetro ideal (no intercambia calor con el medio) con agua y hielo en equilibrio ⇒ 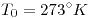
Al agregar 1 Kg de agua a 363°K (=90°C) suponemos como primer paso que se mezcla con el agua presente a 273°K hasta que quedan los 3 Kg de agua a una misma temperatura de equilibrio hasta el momento:

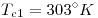
Ahora el hielo comienza a derretirse, suponemos que no llega a consumirse toda la masa de hielo por lo que el sistema terminará a 273°K. Calculo la masa de hielo que se derritió:
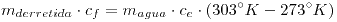
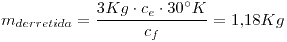
Si la masa hubiese dado más de 2Kg (lo que teníamos de hielo inicialmente) diríamos que la suposición de que el hielo no se derrite completamente no es correcta.
Respondemos que la temperatura de equilibrio es 273°K.
Parte b
Ya que la entropía es función de estado, no importa como haya evolucionado el sistema si no el estado inicial y final. Podríamos calcular la variación de entropía del sistema para los procesos:
1) El agua caliente se enfría
2) El agua fría se calienta
3) El hielo se funde
4) El agua se enfría
Pero para hacer menos cuenta podemos tomar como que el agua que estaba a 0°C no tuvo variación, por lo tanto sólo tomamos:
1) El agua caliente (1Kg) se enfría de 90°C a 0°C
2) El hielo se funde (El agua que se fundió quedó a 0°C así que sólo tomamos el cambio de entropía por la fusión)
Tomamos caminos reversibles para usar la fórmula de cálculo de la entropía para procesos reversibles
 (1)
(1)
Para 1):
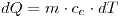
En (1):

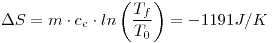
Para 2):

En 1) para T=273°K constante (sale de la integral)
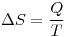
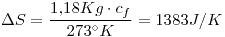
Respondemos:
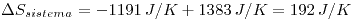
 (por ocurrir el proceso dentro de un calorímetro ideal)
(por ocurrir el proceso dentro de un calorímetro ideal)

