Examen Final - 62.03/62.04 Física IIA/B
Fecha: 2 Cuatrimestre 2004
Día: 21/XII/2004 - TEMA A
Enunciados
- Un Condensador cilíndrico de radios
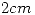 y
y  de largo está conectado a una fuente de
de largo está conectado a una fuente de  (continua). a) Determine la capacidad del condensador, b) ¿Cuál es la carga sobre cada armadura?, c) ¿Cómo se modifican estos valores si se introduce un dieléctrico de constante relativa 5 estando conectado a la batería? d) ¿Cuál es la energía por unidad de longitud del condensador cargado en el último caso?
(continua). a) Determine la capacidad del condensador, b) ¿Cuál es la carga sobre cada armadura?, c) ¿Cómo se modifican estos valores si se introduce un dieléctrico de constante relativa 5 estando conectado a la batería? d) ¿Cuál es la energía por unidad de longitud del condensador cargado en el último caso? - Se tiene un material ferromagnético de permeabilidad
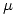 en forma de toroide se sección cuadrada de lado
en forma de toroide se sección cuadrada de lado  y radio interior
y radio interior  , sobre el que se arrollan
, sobre el que se arrollan  vueltas de un conductor. a) Calcule
vueltas de un conductor. a) Calcule  ,
, 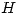 y
y 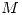 en todo el espacio cuando circula
en todo el espacio cuando circula 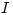 por el arrollamiento; b)Determine la energía almacenada en el material; c) discuta que pasa con esos valores si se corta la corriente y se practica un pequeño entre hierro; d) si se coloca un segundo arrollamiento sobre el toroide de
por el arrollamiento; b)Determine la energía almacenada en el material; c) discuta que pasa con esos valores si se corta la corriente y se practica un pequeño entre hierro; d) si se coloca un segundo arrollamiento sobre el toroide de  vueltas conectado a una resistencia
vueltas conectado a una resistencia  , ¿cuál es la potencia disipada si por la primera bobina circula
, ¿cuál es la potencia disipada si por la primera bobina circula 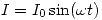
- Se tiene un circuito compuesto por un condensador (
 ) y una inductancia (
) y una inductancia ( ) en paralelo conectados en serie con una resistencia (
) en paralelo conectados en serie con una resistencia ( ), alimentado por una fem
), alimentado por una fem  . Determine a) la impedancia del circuito, b) la potencia disipada en la resistenca, c) las corrientes sobre cada elemento, d) las energías almacendas debidas a los campos eléctricos y magnéticos.
. Determine a) la impedancia del circuito, b) la potencia disipada en la resistenca, c) las corrientes sobre cada elemento, d) las energías almacendas debidas a los campos eléctricos y magnéticos. - (Sólo para Física IIB) Describa y explique el comportamiento ferromagnético de la materia. Analice una curva de histéresis y comente los parámetros que la caracterizan. Diferencie entre materiales magnéticos duros y suaves. Comente sobre la disipación de energía del material en relación a la curva de histéresis. Compare con el comportamiento paramagnético y diamagnético.
- (Sólo para Física IIA) a) Calcular el rendimiento de un ciclo de Carnot y verificar que la variación de entropía es cero en el ciclo; b) Determinar el perfil de temperaturas dentro del aislador si se tiene un tubo cilíndrico de radio exterior
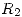 y coeficiente de conducción
y coeficiente de conducción 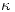 (la pared interior del aislador se encuentra a
(la pared interior del aislador se encuentra a  y la exterior a
y la exterior a  .
. - a) Describir dos métodos para medir la frecuencia de resonancia de un circuito
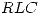 serie con los elementos disponibles en el laboratorio de Física II. Justificar. b) (Sólo para Física IIA)Describa el TP del calorímetro.
serie con los elementos disponibles en el laboratorio de Física II. Justificar. b) (Sólo para Física IIA)Describa el TP del calorímetro.
Resolución
Problema 1
Primero que todo podemos llamar 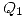 y
y  a las cargas en la placa interior y exterior sobre las paredes del cilindro. Además el enunciado parece estar mal redactado por lo que supondremos que el cilindro es infinito y que la pila está conectada con el borne postivo hacia el exterior.
a las cargas en la placa interior y exterior sobre las paredes del cilindro. Además el enunciado parece estar mal redactado por lo que supondremos que el cilindro es infinito y que la pila está conectada con el borne postivo hacia el exterior.
 o bien que
o bien que 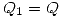 y
y  .
.
Para averiguar la capacidad del sistema debemos calcular la diferencia de potencial entre las placas y la carga acumulada en ellas. Pero la diferencia de potencial es dato (la pila), entonces debo averiguar la carga que hallaremos justamente con el mismo dato.
Sea 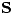 un cilindro matemático de radio
un cilindro matemático de radio  y altura
y altura 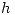 .
Entonces se procederá a usar la ley de Gauss. Para eso primero debe calcularse el flujo de D sobre S.
.
Entonces se procederá a usar la ley de Gauss. Para eso primero debe calcularse el flujo de D sobre S.
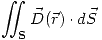
Ahora vamos a considerar la simetría del problema. Esto me dice que 
Como el diferencial de superficie sobre la superficie lateral de la superficie gaussiana en este problema es  entonces el producto queda
entonces el producto queda 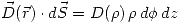 .
.
Ademas en las tapas  , por lo que
, por lo que 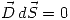
Ahora se calcula el flujo:
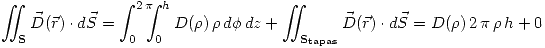
Ahora para utilizar la ley de Gauss debemos calcular la carga encerrada por la superficie  que, como es de prever, dependerá de
que, como es de prever, dependerá de  . También se observa que sólo hay cargas en las superficies de las corazas del condensador.
Así:
. También se observa que sólo hay cargas en las superficies de las corazas del condensador.
Así:

Por lo tanto:

En donde he usado que 
Ahora como  entonces
entonces

Pues en el vacio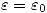
Para calcular el potencial entre las capas calcularemos la circulación de  que, como es de esperar, la haremos por un camino radial.
que, como es de esperar, la haremos por un camino radial. 

Reemplazando  , despejamos
, despejamos 
Entonces cuando queramos usar 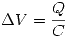 veremos que debemos saber la carga sobre cada placa para calcular la capacidad, lo que es imposible pues esta carga es infinita en este cilindro infinito, por lo tanto lo calcularemos para una altura
veremos que debemos saber la carga sobre cada placa para calcular la capacidad, lo que es imposible pues esta carga es infinita en este cilindro infinito, por lo tanto lo calcularemos para una altura 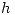 genérica.
genérica.
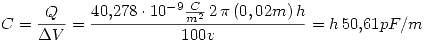
Para el punto b sucede lo mismo, es imposible calcular la carga, pero por lo menos calculamos la densidad de carga  (ya calculada arriba) y
(ya calculada arriba) y 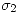 que la sacamos usando la primer relación que escribí:
que la sacamos usando la primer relación que escribí:

Para el punto c nos piden volver a calcular todo si 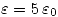 En este caso
En este caso  y la carga sale de
y la carga sale de 
Para el punto d necesitamos calcular la densidad de energía y luego con eso hallar la energía por unidad de longitud. Lo primero es: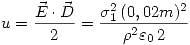
Además 
 Los cálculos los dejo para hacer.
Los cálculos los dejo para hacer.
Problema 2
Parte a
Debo hallar los vectores  ,
, 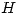 y
y 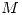 en todo el espacio, pero suponiendo que la permitividad del material es lo suficientemente alta podemos suponer que sólo existiran en la región interior al material.
en todo el espacio, pero suponiendo que la permitividad del material es lo suficientemente alta podemos suponer que sólo existiran en la región interior al material.
En este caso lo que utilizaremos es la ley de Ampère: 
Esto vale para cualquier curva cerrada del espacio. Vamos a tomar una curva 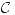 que sea una circunferencia de radio
que sea una circunferencia de radio 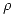 dentro del toroide. En esta curva, como aclaré antes, vamos a suponer que el campo es siempre paralelo a la curva y depende sólo del radio, entonces:
dentro del toroide. En esta curva, como aclaré antes, vamos a suponer que el campo es siempre paralelo a la curva y depende sólo del radio, entonces:  y además que
y además que 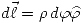 .
.
Así 
Como la corriente que concatena la curva 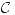 es
es  veces
veces 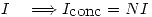 .
.
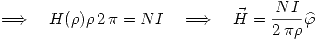
Usando la relación del material 
Para calcular la magenetización uso  Resultando
Resultando 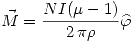 . Como
. Como  .
.
Por lo tanto 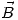 y
y  tienen el mismo sentido y
tienen el mismo sentido y  el sentido contrario.
el sentido contrario.
Parte b
La energía almacenada se calcula viendo primero la densidad de energía 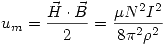
Y como antes 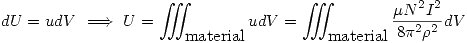
Y como 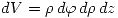 (es una sección de cilindro digamos) entonces:
(es una sección de cilindro digamos) entonces: 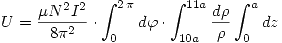
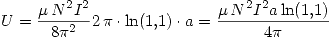
Parte c Se corta la corriente y se realiza un corte.
En estas condicones se mantiene como antes (pues el material es ferromagnético).
se mantiene como antes (pues el material es ferromagnético).

En este caso no hay corriente verdadera, entonces deducimos de la ley de Ampère:  .
.
Por condiciones de contorno al ver que la sección del toroide no cambia 

Obteniendo: 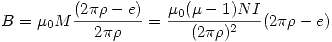 y se ve que
y se ve que  .
.
![<tex>H_M=\frac{(\mu-1)NI}{(2\pi\rho)^2}(2\pi\rho-e)-\frac{(\mu-1)NI}{2\pi\rho}=\frac{(\mu-1)NI}{2\pi\rho}\left [\frac{2\pi\rho-e}{2\pi\rho}-1\right]=-\frac{(\mu-1)NI}{2\pi\rho}\frac{e}{2\pi\rho}</tex> <tex>H_M=\frac{(\mu-1)NI}{(2\pi\rho)^2}(2\pi\rho-e)-\frac{(\mu-1)NI}{2\pi\rho}=\frac{(\mu-1)NI}{2\pi\rho}\left [\frac{2\pi\rho-e}{2\pi\rho}-1\right]=-\frac{(\mu-1)NI}{2\pi\rho}\frac{e}{2\pi\rho}</tex>](lib/plugins/latex/images/b0a558994f9a603f9caca16dc951a00300948889_0.png) .
.
Es decir que  .
.
Y  .
.
Entonces podemos concluír que en el material 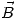 y
y  son paralelos y
son paralelos y  tiene sentido contrario. En el entrehierro
tiene sentido contrario. En el entrehierro  y
y 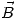 y
y  son paralelos.
son paralelos.
Parte d
En esta parte se calcula el flujo que genera la bobina 1 sobre la bobina 2, es decir: 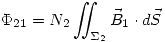 . Entonces:
. Entonces:
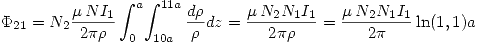
La inductancia mutua es entonces:  .
.
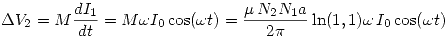

Problema 3
[no pongo el esquema aún]
Parte a
La impedancia del circuito es:
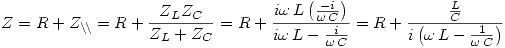
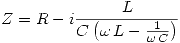
Parte b
Si  y
y 
 (Ley de Kirchoff de Corriente alterna)
(Ley de Kirchoff de Corriente alterna)
De aquí:  y
y 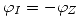

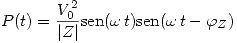
siendo  y
y ![<tex>\varphi_Z=\mathrm{arctg}\left[\frac{-L}{RC\left(\omega\,L-\frac{1}{\omega\,C}\right)}\right]</tex> <tex>\varphi_Z=\mathrm{arctg}\left[\frac{-L}{RC\left(\omega\,L-\frac{1}{\omega\,C}\right)}\right]</tex>](lib/plugins/latex/images/8534c91165bd7db3251330b9788d2aae18ba2c6f_0.png)
Si se mide con un potenciómetro se verá la Potencia aparente:
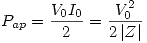
Parte c
Se cumple que si son  y
y  las tensiones y corrientes complejas (es decir que la parte real de ellas es la tensión y la corriente), entonces:
las tensiones y corrientes complejas (es decir que la parte real de ellas es la tensión y la corriente), entonces:
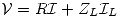



![<tex>\left[\frac{V_0}{\omega\,L}\underbrace{e^{-i\frac{\pi}{2}}}_{-i}- \frac{RI_0}{\omega\,L}e^{i(\varphi_I-\frac{\pi}2)}\right]e^{i\omega\,t}=\mathcal{I}_L</tex> <tex>\left[\frac{V_0}{\omega\,L}\underbrace{e^{-i\frac{\pi}{2}}}_{-i}- \frac{RI_0}{\omega\,L}e^{i(\varphi_I-\frac{\pi}2)}\right]e^{i\omega\,t}=\mathcal{I}_L</tex>](lib/plugins/latex/images/8d7c22cbe0798145aec4a5c3f250fca59953fca9_0.png)
![<tex>\left[-\frac{V_0}{\omega\,L}i-\frac{RI_0}{\omega\,L}\left(\mathrm{cos}\left(\varphi_I-\frac{\pi}2\right)+ i\mathrm{sen}\left(\varphi_I-\frac{\pi}2\right)\right)\right]e^{i\omega\,t}=\mathcal{I}_L</tex> <tex>\left[-\frac{V_0}{\omega\,L}i-\frac{RI_0}{\omega\,L}\left(\mathrm{cos}\left(\varphi_I-\frac{\pi}2\right)+ i\mathrm{sen}\left(\varphi_I-\frac{\pi}2\right)\right)\right]e^{i\omega\,t}=\mathcal{I}_L</tex>](lib/plugins/latex/images/2e96aec97b9bece46636c4afc00c1f9c8a41dbe7_0.png)

Parte d
La energía almacenada en el circuito podemos hallarla averiguando la energía almacenada en el capacitor, en la bobina y en la resistencia.
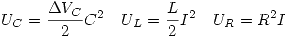
En este problema 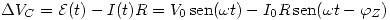
Haciendo la suma de ondas:
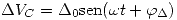
Siendo  y recordando que
y recordando que  . Entonces:
. Entonces:
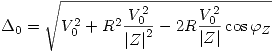
Es decir: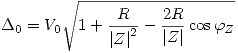
Y ![<tex>\varphi_{\Delta}=\mathrm{arctg}\left[\frac{I_0R\mathrm{sen}(\varphi_Z)}{V_0+RI_0\cos(\varphi_Z)}\right]</tex> <tex>\varphi_{\Delta}=\mathrm{arctg}\left[\frac{I_0R\mathrm{sen}(\varphi_Z)}{V_0+RI_0\cos(\varphi_Z)}\right]</tex>](lib/plugins/latex/images/bceb0f4d3f91063b66096231cedfc5839892066a_0.png)
- Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá o envíame un mail GK



