Examen Parcial - 62.01. Física I - 21/05/2007
Cátedra: 03/Garea
Fecha: 1° Oportunidad - 1° Cuatrimestre 2007
Día: 21/05/2007
Enunciado
Punto I
Una partícula de masa  se mueve en la dirección positiva de las
se mueve en la dirección positiva de las  con una velocidad de
con una velocidad de  . Otra partícula de masa
. Otra partícula de masa  se desplaza en el sentido positivo de las
se desplaza en el sentido positivo de las  con una velocidad de
con una velocidad de  . Ambas partículas se encuentran sobre una mesa horizontal (plano
. Ambas partículas se encuentran sobre una mesa horizontal (plano  ) sin rozamiento en las coordenadas
) sin rozamiento en las coordenadas  para la partícula
para la partícula  , y
, y  para la partícula
para la partícula  .
.
- Calcular la posición del centro de masa en ese instante.
- Calcular el momento cinético (o impulso angular) y la cantidad de movimiento del sistema. ¿Se conservan?
- En un cierto instante las partículas chocan luego de lo cual la primera se mueve con una velocidad de
 , formando un ángulo de
, formando un ángulo de  grados con la dirección
grados con la dirección  (positivo en sentido antihorario). ¿Cuál es la velocidad de la otra partícula luego del choque?
(positivo en sentido antihorario). ¿Cuál es la velocidad de la otra partícula luego del choque? - Este choque, ¿es elástico?
Punto II
 En el diagrama de la figura se muestra un disco de masa
En el diagrama de la figura se muestra un disco de masa 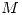 y radio
y radio  , que avanza en el sentido de la fuerza
, que avanza en el sentido de la fuerza  y que rueda sin deslizar. Este cilindro tiene una canaleta a una distancia
y que rueda sin deslizar. Este cilindro tiene una canaleta a una distancia 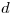 de su borde exterior, y está conectado por medio de una soga inextensible de masa despreciable a una masa puntual
de su borde exterior, y está conectado por medio de una soga inextensible de masa despreciable a una masa puntual  según se indica. Entre el bloque y el plano inclinado se puede despreciar el rozamiento. La fuerza
según se indica. Entre el bloque y el plano inclinado se puede despreciar el rozamiento. La fuerza  está aplicada en el centro de masa del cilindro y se puede considerar que la canaleta es lo suficientemente angosta como para que el momento de inercia del disco corresponda al de un cilindro homogéneo de masa
está aplicada en el centro de masa del cilindro y se puede considerar que la canaleta es lo suficientemente angosta como para que el momento de inercia del disco corresponda al de un cilindro homogéneo de masa 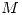 y radio
y radio  .
.
- Realizar el diagrama de cuerpo libre de cada masa y escribir las ecuaciones dinámicas correspondientes.
- Calcular la aceleración del centro de masa del cilindro y la aceleración del cuerpo
 .
. - Si en un instante la velocidad del centro de masa del cilindro es de
 , ¿cuál será la velocidad de la masa
, ¿cuál será la velocidad de la masa  ?
? - ¿Cuál será la energía del sistema disco–masa
 en ese instante? Suponga que el bloque está a una altura
en ese instante? Suponga que el bloque está a una altura 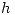 del piso.
del piso.
Datos:  ,
,  ,
,  ,
, 
Punto III
 Un bloque de masa
Un bloque de masa  y que puede considerarse puntual está apoyado sobre una varilla delgada homogénea de masa
y que puede considerarse puntual está apoyado sobre una varilla delgada homogénea de masa  y longitud
y longitud  . El sistema está sostenido por medio de un resorte vertical estirado una distancia
. El sistema está sostenido por medio de un resorte vertical estirado una distancia  , respecto de su posición de equilibrio y el bloque tiene un rozamiento tal que no resbala por la varilla.
Por el punto
, respecto de su posición de equilibrio y el bloque tiene un rozamiento tal que no resbala por la varilla.
Por el punto  pasa un eje por donde puede girar la varilla (sin rozamiento entre el eje y la varilla).
pasa un eje por donde puede girar la varilla (sin rozamiento entre el eje y la varilla).
- Teniendo en cuenta que las masas y las longitudes indicadas son datos, hallar la constante del resorte.
- ¿Cuál será la energía del sistema barra–bloque en ese instante?
- Si se corta el resorte, ¿qué aceleración angular tendrá el sistema en este nuevo instante? Suponga aquí también que el bloque no desliza.
