Examen Parcial - 62.01. Física I - 23/04/2007

Cátedra: 03/Garea
Fecha: 1° Oportunidad - 1° Cuatrimestre 2007
Día: 23/04/2007

El sistema de la figura, formado por dos masas 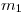y 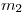se desplaza en el sentido de las positivas de manera tal que la fuerza y el rozamiento entre la partícula y la son tales que la partícula no se desplaza en sentido vertical y ambas se mueven solidarias en el sentido horizontal, con una aceleración de módulo .

1. Realizar el diagrama de cuerpo libre de cada cuerpo e indicar todos los pares de interacción de las fuerzas actuantes en ambos cuerpos.
2. Calcular el valor de y la fuerza de rozamiento entre y . ¿Es esta fuerza la máxima posible para este movimiento?
3. Calcular el trabajo de y el trabajo de la fuerza de contacto entre sobre cuando cada masa se desplaza 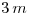de su posición inicial. ¿Cuánto vale la variación de energía cinética de la partícula .

Datos: , 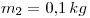. , tanto entre y como entre y el piso.

Un bloque pasa por una pista como la esquematizada en la figura, moviéndose desde el punto hasta entrar en una curva de radio con un peralte de inclinación .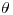
El tramo 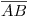tiene una longitud y se encuentra a una altura 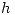respecto del plano del círculo descrito en el peralte. En el punto el bloque se encuentra apoyado en un resorte, de constante 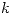, comprimido una longitud , respecto de su posición de equilibrio. En toda la pista el rozamiento es despreciable, incluso en la curva.

1. Calcular la velocidad con la que el móvil entra en la curva.
2. Calcular la inclinación 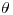necesaria en el peralte para que el bloque no se desplace lateralmente en la curva.

Responder solamente uno de los siguientes puntos:

1. El centro de la Luna está a 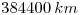del centro de la Tierra y completa su órbita circular alrededor de la misma en 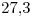días.
   1. Determinar el módulo de la velocidad de la Luna respecto de la Tierra.
   2. Determinar la posición de un punto entre la Tierra y la Luna, medida desde la Tierra, en la cual una partícula de masa tiene fuerza neta nula.
      

En ambos casos considere que las fuerzas de otros cuerpos celestes son despreciables.
Datos: la gravedad sobre la superficie de la Luna es de la gravedad sobre la superficie de la Tierra y el radio de la Luna es del radio terrestre.

1. El módulo de la fuerza neta que actúa sobre una partícula que realiza un movimiento rectilíneo sobre el eje varía con la posición, como indica la figura. La fuerza forma, en todo el trayecto, un ángulo de con respecto a la horizontal .
   1. Calcular el trabajo realizado por dicha fuerza en el trayecto de a
   2. ¿Aumentó o disminuyó su velocidad en dicho trayecto?
   3. ¿Qué potencia media desarrolló dicha fuerza si el tiempo transcurrido en el trayecto es de ?