Examen Final - 62.01. Física I - 05/07/2011
- Enunciado
  - Punto 1
  - Punto 2
  - Punto 3
  - Punto 4
- Resolución
  - Punto 1
  - Punto 2
  - Punto 3
- Discusión

2011

Cátedra: Mismo coloquio para todas las cátedras
Fecha: 2º Oportunidad - 1º Cuatrimestre 2011
Día: 05/07/2011
Tema: 1

Thread del foro

Puede ser que haya errores en los enunciados ya que no se copiaron directamente del coloquio. Si alguien los tiene, es bienvenido a modificarlos.

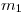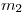Tenés dos partículas ( $<tex>m_1</tex>$ y $<tex>m_2</tex>$ ) con velocidades 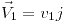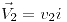$<tex> \vec{V}_1 = v_1 j </tex>$ ; $<tex> \vec{V}_2 = v_2 i </tex>$ y te daba la relación $<tex>m_1=m_2</tex>$ y chocaban plásticamente. Pedía sacar:

a)	Velocidad Final del sistema, y la trayectoria después de la colisión de las 2 partículas.
b)	Calcular el momento angular respecto del origen y respecto del CM. Comparar los resultados.

Punto 2

Dos cilindros de radio R y masa M están unidos por un perno de radio r y masa m (cilindro menor que los otros 2 cilindros) y rueda sin resbalar sobre un plano inclinado.

Te dan el momento de inercia de un cilindro respecto del CM : 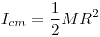$<tex> I_{cm}=\frac{1}{2}MR^2</tex>$

a)	Hallar el momento de inercia del sistema
b)	Hallar la aceleración del centro de masa y Fuerza de rozamiento en función de los datos.
c)	¿Se conserva la energía mecánica del sistema sobre los puntos de contacto?. ¿se conserva el momento angular respecto del CM sobre los puntos de contacto?

Punto 3

Se tiene una cuerda de un violoncelo de 80 cm de longitud. Se quiere cambiar el tono de la onda a 6/5 de la frecuencia inicial.

a)	¿Cuanto se debe acotar la longitud de la cuerda para obtener dicha frecuencia?
b)	¿De qué tipo de onda se trata? Escribir una posible ecuación para cada longitud.

Punto 4

a)

Un objeto se encuentra a 50 cm de una pantalla. Se quiere obtener a traves de una dioptra convergente que separa a los dos medios ( $<tex> n_1=1</tex>$ $<tex> n_2=1.2</tex>$ ) una imagen nitida y real.La dioptra tiene el foco imagen a 24cm.
¿A que distancia respecto del objeto debe colocarse la dioptra para obtener la imagen nitida sobre la pantalla? ¿Que tipo de imagen se obtiene?

b)

Se tiene una luz monocromática que pasa por una ranura de ancho a y longitud de onda λ, se tiene la distancia D de la ranura hasta la pantalla que es lo suficientemente grande (creo que así lo decía).

i)	Indicar la distribución de intensidades sobre la pantalla. que ocurre con la distribución de la intensidad de onda si:
ii)	se disminuye a a la mitad
iii)	se disminuye λ a la mitad decía que justifiquemos con gráficos, expresiones y deducciones.

Resolución

Punto 1

Parte A

Primero, pusimos conservación de la cantidad de movimiento justificando que al no haber fuerzas externas:
$<tex>\sum{F_{ext}}=0 \to F=\frac{dP}{dt} \to \int F \, dt = \int dP \to \int 0 \, dt = \Delta P \to \Delta P = 0 </tex>$

Con esto, y sabiendo que $<tex> m_1 = m_2 </tex>$ aplico:
$<tex> \vec{P}_0 = \vec{P}_f </tex>$ dejando como incógnita la velocidad final pedida.

Y, separando la ecuación para cada eje, me da: 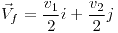$<tex> \vec{V}_f=\frac{v_1}{2} i + \frac{v_2}{2} j </tex>$

Como después del choque, las dos masas están unidas, su trayectoria es la misma que la del centro de masa.

$<tex> \vec{V}_{cm} = \vec{V}_f = \frac{v_1}{2} i + \frac{v_2}{2} j </tex>$
$<tex> \vec{X}^f_{cm} = x_0 i + y_0 j = \vec{X}_1 = \vec{X}_2 </tex>$

Determino el tipo de movimiento:
$<tex> \vec{V}_{cm} = \frac{\Delta P}{\sum m} = \frac{0}{\sum m} = 0 </tex>$

Por lo tanto es un movimiento rectilíneo uniforme. La trayectoria es:

$<tex> \vec{V}_{cm} = \frac{\vec{X} - \vec{X}_{cm}}{\Delta t} </tex>$
$<tex> \vec{X} = \vec{V}_{cm} \Delta t + \vec{X}_{cm} </tex>$

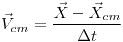
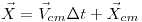
Parte B

Para el momento angular, tenemos:
$<tex> \vec{L}_0 = \sum{\vec{r} \times \vec{P}}= \vec{r}_1 \times \vec{P}_1 + \vec{r}_2 \times \vec{P}_2 = m_1 \left( \vec{r}_1 \times \vec{V}_1\right) + m_1 \left( \vec{r}_1 \times \vec{V}_1\right) = 2 m_1 \left( \vec{X}_{cm} \times \vec{V}_f\right) </tex>$

$<tex> \vec{L}_{cm} = \vec{r}_{cm} \times \vec{P}_{cm} = \sum_i m_i \left(\vec{X}_{cm} \times \vec{V}_{cm} \right) = 2 m_1 \left(\vec{X}_{cm} \times \vec{V}_f\right) </tex>$

$<tex> \vec{L}_0 = \vec{L}_{cm} </tex>$

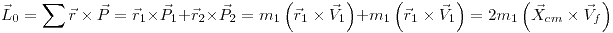
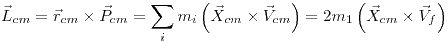
Punto 2

Parte A

Para hallar el momento de inercia del sistema respecto de su CM, tomamos la suma de los tres momentos de inercia de los cilindros porque los tres tienen el mismo eje de simetría.
$<tex>I^\text{cm}_\text{sist} = \frac{1}{2} MR^2 + \frac{1}{2} m r^2+ \frac{1}{2} MR^2=MR^2 + \frac{1}{2} m r^2 </tex>$

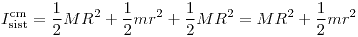
Parte B

Aplico sumatoria de fuerzas en el eje x, tomando a este como paralelo al plano (sumo la fuerza de la gravedad y la de rozamiento.
$<tex> \sum{F_x}= m_T a_\text{cm} \to \sum{F_x}= P_x -F_\text{roz} = m_T g \sen (\alpha) -F_\text{roz} = m_T a_\text{cm}</tex>$

Como rueda sin resbalar, uso la condición de rodadura:
$<tex> a_{cm} = \gamma r \to \gamma = \frac{a_{cm}}{r} </tex>$

Aplico suma de momentos:
$<tex> \left| \sum{\vec{M}} \right| = \left| \vec{F}_\text{roz} \right| </tex>$ $<tex>\left| \vec{r} \right| </tex>$ $<tex>\left| \sen{\beta_{\vec{F}_\text{roz}, \vec{r}}} \right| </tex>$ $<tex>= \gamma I^\text{cm}_\text{sist} = \frac{a_\text{cm}}{r} I^\text{cm}_\text{sist} \to F_\text{roz}=\frac{a_\text{cm} I^\text{cm}_\text{sist}}{r^2}</tex>$

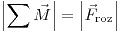
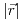
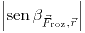
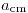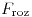Finalmente, quedan dos ecuaciones (la suma de fuerzas y la suma de momentos) con dos incognitas ( $<tex>a_\text{cm}</tex>$ y $<tex>F_\text{roz}</tex>$ ) y se resuelve el sistema:
1) $<tex>m_T g \sen \left( \alpha \right) - F_\text{roz} = m_T a_\text{cm}</tex>$
2) $<tex>F_\text{roz}=\frac{a_\text{cm} I^\text{cm}_\text{sist}}{r^2}</tex>$

$<tex>a_\text{cm}= \frac{m_T g \sen \left(\alpha\right)}{m_T+\frac{I^\text{cm}_\text{sist}}{r^2}}</tex>$
$<tex>F_\text{roz}= \frac{m_T g \sen \left(\alpha\right)}{1+\frac{r^2}{I^\text{cm}_\text{sist}}}</tex>$

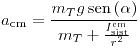
Parte C

Para ver si se conserva la energía mecánica, veo si hay trabajo de fuerzas conservativas, ya que: $<tex> \Delta E_m = W_{\vec{F}_{NC}} </tex>$

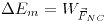
Como el punto de contacto es un CIR (centro instantáneo de rotación), su velocidad es igual a 0 y por lo tanto no hay traslación. Al no haber traslación, el trabajo de todas las fuerzas serán iguales a 0. Entonces, la energía mecánica se conserva.

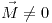Respecto del punto de contacto, $<tex>P_x</tex>$ realiza momento sobre el punto de contacto. Por lo tanto $<tex> \vec{M} \neq 0 </tex>$ y entonces el momento angular no se conserva. $<tex> \vec{M}=\frac{d\vec{L}}{dt} </tex>$

Punto 3

Parte A

Como se trata de una cuerda de un violoncelo, se encuentra fija a sus extremos y por lo tanto los extremos son nodos de vibración. Al ser estos los únicos nodos, suena a una frecuencia fundamental:
$<tex> \lambda = 2L </tex>$
$<tex>f = \frac{v}{\lambda} = \frac{v}{2L} </tex>$

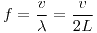
La velocidad de propagación es la misma para antes y después de acortar la longitud ya que depende del material (que suponemos que es homogéneo).
Si se quiere cambiar la frecuencia a 6/5 respecto de la inicial:
$<tex> f_2 = 6/5 f_1 </tex>$

$<tex> \left. \begin{array}{ll} v = \lambda_1 f_1 \\ v = \lambda_2 f_2 \end{array} \right\} \to \lambda_2 \frac{6}{5} f_1 = \lambda_1 f_1 \to 2 L_2 \frac{6}{5} = 2 L_1 \to L_2 = \frac{5}{6} L_1 = \frac{5}{6} 80\mbox{ cm} \approx 66.6 \mbox{ cm}</tex>$

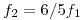
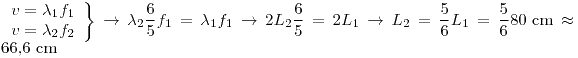
Parte B

Se trata de una onda estacionaria.

$<tex> \epsilon_1 = 2 \epsilon_0 \sen \left(k_1 x \right) \cos \left( k_1 c t \right) </tex>$
$<tex> \epsilon_2 = 2 \epsilon_0 \sen \left(k_2 x \right) \cos \left( k_2 c t\right) </tex>$

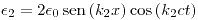
con el número de onda $<tex> k = \frac{\pi}{L} </tex>$

Discusión

Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.