Tabla de Contenidos
Examen Parcial - 61.13. Análisis Matemático III C
Cátedra: Todas
Fecha: 1º Oportunidad - (2º Cuatrimestre) 2007
Día: 09/11/2007
Punto I
Hallar 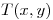 y calcular
y calcular 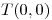
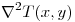 en
en ![<tex>D= \left[ \begin{array}{cc} x^2+y^2=1, y>0\\ (y-1)^2+x^2=2,y<0 \\ \end{array} \right]</tex> <tex>D= \left[ \begin{array}{cc} x^2+y^2=1, y>0\\ (y-1)^2+x^2=2,y<0 \\ \end{array} \right]</tex>](lib/plugins/latex/images/2e9a7e85dcaa9a40dbadc2251c6964f3395c28b5_0.png)
 para
para 
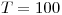 para
para 
Punto II
Determinar para qué valores de  entero la siguiente integral converge o tiene valor principal, y calcularlos:
entero la siguiente integral converge o tiene valor principal, y calcularlos:
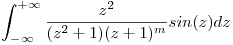
Punto III
Si la función u(xy) fuera armónica calcular su armónica conjugada:
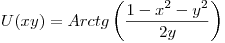
Punto IV
En el punto 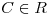 hay una fuente de flujo cuyo potencial complejo es
hay una fuente de flujo cuyo potencial complejo es 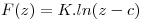
(a) Si se introduce un cilindro 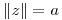 demostrar que el flujo resultante tiene un potencial complejo
demostrar que el flujo resultante tiene un potencial complejo 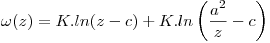 .
.
(b) Calcular la fuerza que actúa sobre el cilindro. ¿Hacia dónde se desplazará el cilindro?
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
