Examen Parcial - 61.12. Análisis III B - 21/11/2006
Cátedra: González
Fecha: Segunda Oportunidad - Segundo Cuatrimestre 2006
Día: 21/11/2006
Enunciado
Ejercicio I
- Analizar continuidad y derivabilidad de
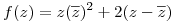 .
. - Dar la imagen de
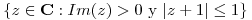 al aplicar
al aplicar 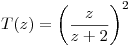 .
. - ¿Qué funciones
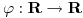 cumplen que
cumplen que 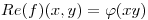 es la parte real de una función
es la parte real de una función  entera? Hallar
entera? Hallar 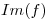 .
.
Ejercicio 2
- Hallar la región Adel plano en donde
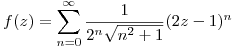 es holomorfa y calcular
es holomorfa y calcular 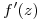 para todo
para todo 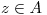
- Sean
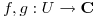 funciones holomorfas en
funciones holomorfas en 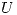 abierto y conexo. Además existe una sucesión
abierto y conexo. Además existe una sucesión 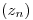 en U convergente a
en U convergente a 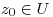 tal que para todo
tal que para todo 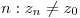 ,
, 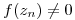 ,
, 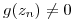 y
y 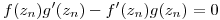 . Probar que existe una constante
. Probar que existe una constante  tal que
tal que  . (Sug.: derivada del cociente)
. (Sug.: derivada del cociente) - Desarrollar la función
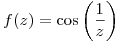 en serie de Laurent en potencias de
en serie de Laurent en potencias de  y obtener
y obtener 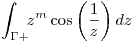 para
para 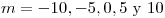 , siendo
, siendo 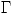 contorno cerrado con
contorno cerrado con 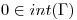
Ejercicio 3
- Sea la ecuación diferencial ordinaria dada por
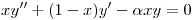 ,
, 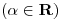 . Mostrar que
. Mostrar que  es un punto de Fuchs pero existe una función analítica solución de la ecuación.
es un punto de Fuchs pero existe una función analítica solución de la ecuación. - Calcular
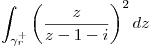 siendo
siendo 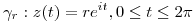 para todos los valores de
para todos los valores de 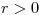 que sea posible.
que sea posible. - Estudiar qué tipo de singularidad tiene
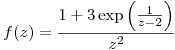 en
en 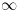 y hallar
y hallar ![<tex>Res[f,\infty]</tex> <tex>Res[f,\infty]</tex>](lib/plugins/latex/images/783f44074ea8166c438932cb1a6c7eb074af9135_0.png)
Resolución
Ejercicio I
Punto 1
Como  y
y 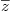 son continuas,
son continuas,  es contua en todo el plano por ser combinación de estas funciones.
Desarrollando:
es contua en todo el plano por ser combinación de estas funciones.
Desarrollando:
![<tex>f(z)=(x+iy)(x-iy)^2+2(x+iy-x+iy)=\underbrace{x(x^2+y^2)}_{u(x,y)}+i\underbrace{[-y(x^2+y^2)+4y]}_{v(x,y)}</tex> <tex>f(z)=(x+iy)(x-iy)^2+2(x+iy-x+iy)=\underbrace{x(x^2+y^2)}_{u(x,y)}+i\underbrace{[-y(x^2+y^2)+4y]}_{v(x,y)}</tex>](lib/plugins/latex/images/471aa1392d4cab66d18acebb3ed3bcb51e673b71_0.png) .
.
Como u y v son polinomios entonces son diferenciables, entonces f será derivable donde se cumplan las conficiones de Cauchy-Riemann.
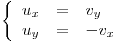
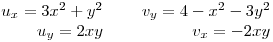
Se observa que la segunda ecuación se cumple en todo el plano, y la primera ecuación da:
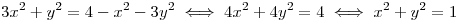
Entonces f sólo será derivable en la circunferencia de centro  y radio 1.
y radio 1.
Punto 2
Punto 3
Ejercicio 2
Punto 1
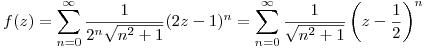
Es una serie de potencias alrededor de 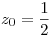 , con término
, con término 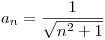 .
Por propiedad de este tipo de series puedo buscar su radio de convergencia asegurando la convergencia absoluta en los puntos del interior de un círculo de centro
.
Por propiedad de este tipo de series puedo buscar su radio de convergencia asegurando la convergencia absoluta en los puntos del interior de un círculo de centro 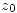 y divergencia en su exterior.
y divergencia en su exterior.
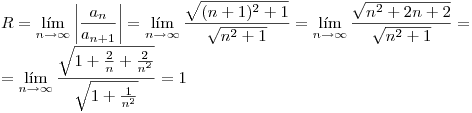
Entonces la serie converge en  , y no converge en
, y no converge en  .
Para los puntos
.
Para los puntos  no se puede decir nada a priori.
no se puede decir nada a priori.
Por la unicidad del desaroollo de Taylor puedo decir que la serie dada es el desarrollo de Taylos de f, lo que garantiza que f sea holomorfa en  . En este caso no interesa la convergencia en
. En este caso no interesa la convergencia en  , pued f solo puede ser holomorfa en conjuntos abiertos. Entonces:
, pued f solo puede ser holomorfa en conjuntos abiertos. Entonces:
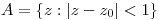 con
con 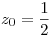 .
.
La convergencia uniforme me permite derivar término a término, entonces:
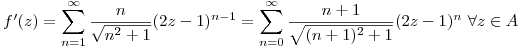
siendo f' también holomorfa en A.
Punto 2
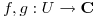 holomorfas en U abierto y conexo,
holomorfas en U abierto y conexo, 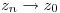
Sea ![<tex>h(z)=\frac{f(z)}{g(z)} \Longrightarrow h'(z)=\frac{g(z)f'(z)-f(z)g'(z)}{[f(z)]^2}</tex> <tex>h(z)=\frac{f(z)}{g(z)} \Longrightarrow h'(z)=\frac{g(z)f'(z)-f(z)g'(z)}{[f(z)]^2}</tex>](lib/plugins/latex/images/09f8f4b6a9409e4398fcd24aa6b4666fd7e71527_0.png)
Como 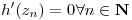 por el principio de indentidad (como
por el principio de indentidad (como 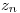 converge a
converge a 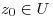 )
)
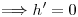 en todo U.
Como U es abierto y conexo entonces
en todo U.
Como U es abierto y conexo entonces  cte, por lo tanto
cte, por lo tanto 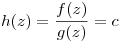 , y entonces
, y entonces  .
.
