Examen Parcial - 61.12. Análisis III B - 25/11/2005
Cátedra: González
Fecha: Tercera Oportunidad - Segundo Cuatrimestre 2005
Día: 25/11/2005
Enunciado
Ejercicio 1
a) Estudiar la derivabilidad de 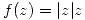 en todo su dominio.
en todo su dominio.
b) Probar que si f es entera y 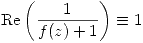 entonces f es identicamente nula.
entonces f es identicamente nula.
c) Hallar todos los puntos donde 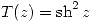 es conforme ¿Qué ángulo forman en su intersección las imágenes por T de las rectas
es conforme ¿Qué ángulo forman en su intersección las imágenes por T de las rectas 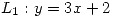 y
y 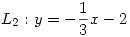
Ejercicio 2
a) Mostrar que  es holomorfa en
es holomorfa en 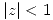 y calcular
y calcular 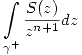 para
para 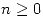 , siendo
, siendo 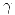 una curva simple y cerrada contenida en
una curva simple y cerrada contenida en 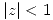 .
.
b) Determinar el término general y la región de convergencia de la serie de Laurent centrada en 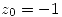 de
de 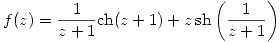 .
.
c) ¿Admite la función 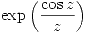 desarrollo de Laurent en
desarrollo de Laurent en 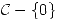 con infinitos términos tanto de exponentes positivos como de exponentes negativos? ¿Por qué?.
con infinitos términos tanto de exponentes positivos como de exponentes negativos? ¿Por qué?.
Ejercicio 3
a) Para 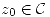 , sea
, sea 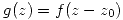 . Probar que si 0 es polo de orden m de f, entonces
. Probar que si 0 es polo de orden m de f, entonces 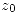 es polo de orden m de g y
es polo de orden m de g y ![<tex>\mathrm{Res}[g,z_0]=\mathrm{Res}[f,0]</tex> <tex>\mathrm{Res}[g,z_0]=\mathrm{Res}[f,0]</tex>](lib/plugins/latex/images/3f5afe0c6ad475a6b59089702a88c66f34b10b02_0.png) .
.
b) Clasificar todas las singularidades en 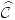 de
de 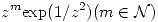 y hallar el residuo en cada una de ellas.
y hallar el residuo en cada una de ellas.
c) Calcular 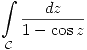 siendo
siendo 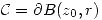 con
con 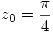 y
y 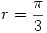 .
.
Resolución
Ejercicio I
Parte a
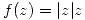
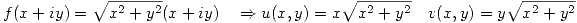
Además u y v son diferenciables para todo 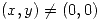 entonces las condiciones de Cauchy-Riemman garantizan la derivabilidad de f. Ahora chequearemos que puntos las cumplen.
entonces las condiciones de Cauchy-Riemman garantizan la derivabilidad de f. Ahora chequearemos que puntos las cumplen.
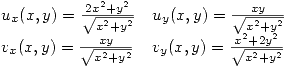
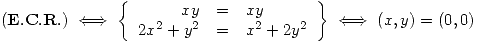
Pero en este punto no valen estas derivadas parciales, por lo que debo ver si es derivable por la definición.
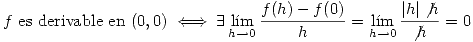
Por lo tanto f es derivable en el 0 y 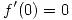 .
.
Parte b
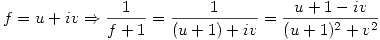
…
Parte c
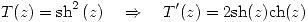
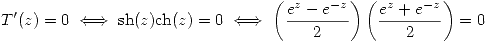
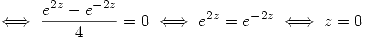
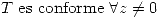
Como  y
y  no pasan por el origen entonces su intersección no es el origen y la transformación será conforme en este punto. Entonces el ángulo de las imágenes de las rectas en este punto será igual al ángulo entre las rectas. Por tener pendientes inversas, estás rectas son perpendiculares:
no pasan por el origen entonces su intersección no es el origen y la transformación será conforme en este punto. Entonces el ángulo de las imágenes de las rectas en este punto será igual al ángulo entre las rectas. Por tener pendientes inversas, estás rectas son perpendiculares: 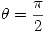
Ejercicio 2
Parte a
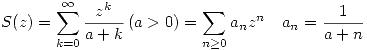
Por propiedad de las series de potencias 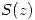 converge en todo punto interior al cículo de radio de convergencia
converge en todo punto interior al cículo de radio de convergencia 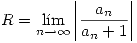
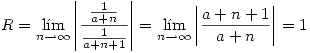
Por lo tanto S converge absoluta y uniformemente 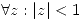 . Esto define una función holomorfa
. Esto define una función holomorfa 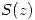 en toda esta región (abierta).
en toda esta región (abierta).
Por la fórmula integral de Cauchy:
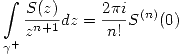 .
.
Para este caso por Taylor vale: 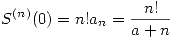 . Entonces:
. Entonces:
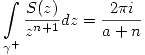
Parte b
![<tex>\begin{array}{rcl} f(z) & = & \displaystyle \frac{1}{z+1} \mathrm{ch}(z+1) + z \, \mathrm{sh} \left( \frac{1}{z+1} \right) \\ & = & \displaystyle (z+1)^{-1}\mathrm{ch}(z+1)+(z+1)\mathrm{sh}[(z+1)^{-1}]-\mathrm{sh}[(z+1)^{-1}] \end{array}</tex> <tex>\begin{array}{rcl} f(z) & = & \displaystyle \frac{1}{z+1} \mathrm{ch}(z+1) + z \, \mathrm{sh} \left( \frac{1}{z+1} \right) \\ & = & \displaystyle (z+1)^{-1}\mathrm{ch}(z+1)+(z+1)\mathrm{sh}[(z+1)^{-1}]-\mathrm{sh}[(z+1)^{-1}] \end{array}</tex>](lib/plugins/latex/images/337cf4eda289c5c909eb5924d352e978c1081fc0_0.png)
Ahora recordando la serie de la exponencial deduciremos las series de las funciones hiperbólicas.
![<tex>\begin{array}{rcl} \mathrm{ch}(w) & = & \frac{e^w+e^{-w}}{2} \\& = & \frac{1}{2} \sum_{n=0}^{\infty} \left( \frac{w^n}{n!} + \frac{(-1)^{n}w^n}{n!} \right) \\& = & \frac{1}{2} \left[ \frac{w^0}{0!}+\frac{w^0}{0!}+\frac{w^1}{1!}-\frac{w^1}{1!}+\frac{w^2}{2!}+\frac{w^2}{2!}+ \frac{w^3}{3!}-\frac{w^3}{3!}+... \right] \\& = & \frac{w^0}{0!}+\frac{w^2}{2!}+\frac{w^4}{4!}+...\\& = & \sum_{n=0}^{\infty} \frac{w^{2n}}{(2n)!} \end{array}</tex> <tex>\begin{array}{rcl} \mathrm{ch}(w) & = & \frac{e^w+e^{-w}}{2} \\& = & \frac{1}{2} \sum_{n=0}^{\infty} \left( \frac{w^n}{n!} + \frac{(-1)^{n}w^n}{n!} \right) \\& = & \frac{1}{2} \left[ \frac{w^0}{0!}+\frac{w^0}{0!}+\frac{w^1}{1!}-\frac{w^1}{1!}+\frac{w^2}{2!}+\frac{w^2}{2!}+ \frac{w^3}{3!}-\frac{w^3}{3!}+... \right] \\& = & \frac{w^0}{0!}+\frac{w^2}{2!}+\frac{w^4}{4!}+...\\& = & \sum_{n=0}^{\infty} \frac{w^{2n}}{(2n)!} \end{array}</tex>](lib/plugins/latex/images/9175dbf7e22386efcd33501473dadf9fbef8aee0_0.png)
![<tex>\begin{array}{rcl} \mathrm{sh}(w) & = & \frac{e^w-e^{-w}}{2} \\& = & \frac{1}{2} \sum_{n=0}^{\infty} \left( \frac{w^n}{n!} - \frac{(-1)^{n}w^n}{n!} \right) \\& = & \frac{1}{2} \left[ \frac{w^0}{0!}-\frac{w^0}{0!}+\frac{w^1}{1!}+\frac{w^1}{1!}+\frac{w^2}{2!}-\frac{w^2}{2!}+ \frac{w^3}{3!}+\frac{w^3}{3!}+... \right] \\& = & \frac{w^1}{1!}+\frac{w^3}{3!}+\frac{w^5}{5!}+...\\& = & \sum_{n=0}^{\infty} \frac{w^{2n+1}}{(2n+1)!} \end{array}</tex> <tex>\begin{array}{rcl} \mathrm{sh}(w) & = & \frac{e^w-e^{-w}}{2} \\& = & \frac{1}{2} \sum_{n=0}^{\infty} \left( \frac{w^n}{n!} - \frac{(-1)^{n}w^n}{n!} \right) \\& = & \frac{1}{2} \left[ \frac{w^0}{0!}-\frac{w^0}{0!}+\frac{w^1}{1!}+\frac{w^1}{1!}+\frac{w^2}{2!}-\frac{w^2}{2!}+ \frac{w^3}{3!}+\frac{w^3}{3!}+... \right] \\& = & \frac{w^1}{1!}+\frac{w^3}{3!}+\frac{w^5}{5!}+...\\& = & \sum_{n=0}^{\infty} \frac{w^{2n+1}}{(2n+1)!} \end{array}</tex>](lib/plugins/latex/images/7b3324fd120e1d0400f6600ac64e178dc1c66c74_0.png)
Ahora se reemplaza en la función:
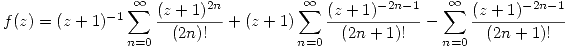
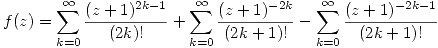
Si quiero escribir a la función como 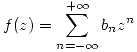 entonces:
entonces:

