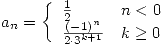Examen Parcial - 61.12. Análisis Matemático III B
Cátedra: González
Fecha: Tercera Oportunidad - Primer Cuatrimestre 2005
Día: 05/07/2005
Enunciado
Punto I
a) ¿Es derivable 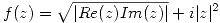 en
en  ?. ¿Por qué?
?. ¿Por qué?
b) Probar que la función  es armónica y dar su conjugada armónica. (Sug.: considerar
es armónica y dar su conjugada armónica. (Sug.: considerar 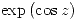 ).
).
c) Sea 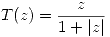 . Demostrar que
. Demostrar que 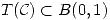 . ¿Existe
. ¿Existe  tal que
tal que 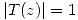 ?. Analizar en qué son transformados los ejes cartesianos al aplicar
?. Analizar en qué son transformados los ejes cartesianos al aplicar  .
.
Punto II
a) Sabiendo que la serie 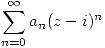 tiene radio de convergencia igual a 2, decir si es posible, si converge o no en los puntos
tiene radio de convergencia igual a 2, decir si es posible, si converge o no en los puntos 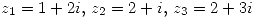 .
.
b) Sea 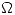 abierto y conexo en
abierto y conexo en 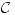 y
y 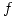 holomorfa en
holomorfa en  con
con 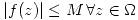 . Probar que
. Probar que 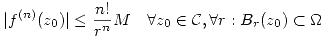 .
.
c) Para 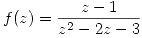 . determinar cuántos desarrollos distintos en potencias de
. determinar cuántos desarrollos distintos en potencias de  admite y en qué región del plano tiene validez cada uno de ellos. Hallar el desarrollo que converge en
admite y en qué región del plano tiene validez cada uno de ellos. Hallar el desarrollo que converge en  .
.
Punto III
a) Clasificar en  las singularidades de
las singularidades de 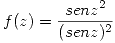 .
.
b) Si  es polo de orden
es polo de orden 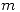 de
de 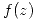 , hallar
, hallar ![<tex>\mathrm{Res}[\mathrm{sen}(z)\frac{f'(z)}{f(z)},z=0]</tex> <tex>\mathrm{Res}[\mathrm{sen}(z)\frac{f'(z)}{f(z)},z=0]</tex>](lib/plugins/latex/images/5a93118d70d01ae5810b6cd1a9cac9ebff6b5097_0.png) .
.
c) Calcular 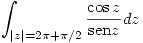 ¿Y si se integra la misma función sobre la curva
¿Y si se integra la misma función sobre la curva 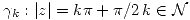 ?.
?.
Resolución
Punto I
Parte a
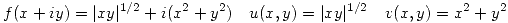
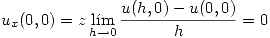
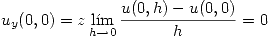
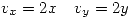
Las condiciones de Cauchy-Riemann se cumplen, pero no puedo afirmar nada sin asegurarme la diferenciabilidad de 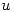 . Por definición
. Por definición 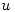 es diferenciable si existe el límite:
es diferenciable si existe el límite:
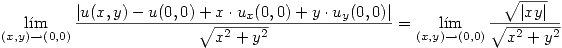
Para evaluar si existe este límite elijo un camino arbitrario 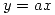 para acercarme al límite, y si el límite depende de
para acercarme al límite, y si el límite depende de  entonces, el límite no existe.
entonces, el límite no existe.
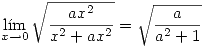 que depende de a, entonces: no existe el límite doble y
que depende de a, entonces: no existe el límite doble y  no es diferenciable en
no es diferenciable en  .
.
Por lo tanto no podemos usar las ecuaciones de Cauchy-Riemann en ese punto. Entonces hay que calcular la derivada por definición:
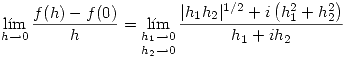
Para demostrar que este límite no existe usaremos la misma técnica que antes. Haremos que 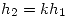 entonces:
entonces:
![<tex> \lim_{h_1\to 0} \left[ \frac{|k|^{1/2}|h_1|}{(1+ki)h_1} + i \underbrace{\left( \frac{1+k^2}{1+ki} \right) h_1}_{\rightarrow 0} \right] </tex> <tex> \lim_{h_1\to 0} \left[ \frac{|k|^{1/2}|h_1|}{(1+ki)h_1} + i \underbrace{\left( \frac{1+k^2}{1+ki} \right) h_1}_{\rightarrow 0} \right] </tex>](lib/plugins/latex/images/e6bea00dabfc5e5f20b88b8e27bc5d4fb49979b1_0.png)
Pero este límite no existe pues:
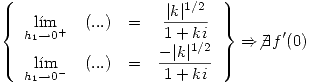
Entonces f no es derivable en 0.
Parte b
Sea 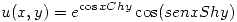 .
.
Consideremos 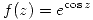 . Desarrollando
. Desarrollando 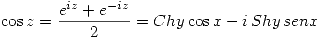
Entonces: ![<tex>f(z)=e^{Chy\cos{x}-i\, Shy\, senx}=e^{Chy\cos{x}} \left[ \cos{(Shy\, senx)} -i\,sen (Shy\, senx) \right] </tex> <tex>f(z)=e^{Chy\cos{x}-i\, Shy\, senx}=e^{Chy\cos{x}} \left[ \cos{(Shy\, senx)} -i\,sen (Shy\, senx) \right] </tex>](lib/plugins/latex/images/f845e40dbbff314d8b5be109c1b1d5a46705d6fb_0.png)
Se observa entonces que ![<tex> u(x,y)=\mathrm{Re}[f(x+iy)] </tex> <tex> u(x,y)=\mathrm{Re}[f(x+iy)] </tex>](lib/plugins/latex/images/04bd8eda9267007ad0f7e936bbc53614ac8c79fb_0.png) . Además
. Además  es enter por ser composición de funciones enteras. Por lo tanto se puede afirmar que
es enter por ser composición de funciones enteras. Por lo tanto se puede afirmar que 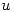 es armónica
es armónica  .
.
La conjugada armónica será entonces la parte imaginaria, es decir: 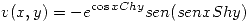 es conjugada armónica.
es conjugada armónica.
Parte c
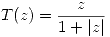
Si 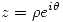 , entonces:
, entonces: 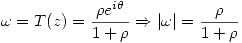 que es siempre menor que 1. Entonces
que es siempre menor que 1. Entonces 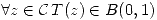
Además no existe ningún 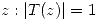 pues
pues 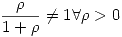 .
.
Por último el eje real se transforma según: 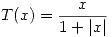 Entonces se transforma en el segmento (-1,1) del plano uv. El eje imaginario
Entonces se transforma en el segmento (-1,1) del plano uv. El eje imaginario 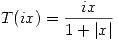 , es decir que se transforma en el segmento (-i,i) del plano uv.
, es decir que se transforma en el segmento (-i,i) del plano uv.
Punto II
Parte a
El teorema del Radio de Convergencia nos dice que si una serie de potencias 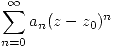 tiene radio de convergencia igual a
tiene radio de convergencia igual a 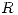 , entonces
, entonces 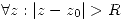 la serie diverge y que
la serie diverge y que 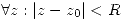 la serie converge absoluta y uniformemente a una función holomorfa. Si
la serie converge absoluta y uniformemente a una función holomorfa. Si 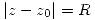 no puedo asegurar la convergencia ni la divergencia en
no puedo asegurar la convergencia ni la divergencia en 
En este caso 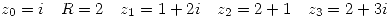 , entonces:
, entonces:
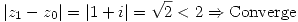
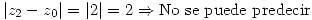
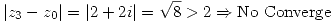
Parte b
Sea 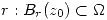 Como
Como 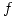 es holomorfa en \Omega abiero y conexo vale la fórmula integral de Cauchy:
es holomorfa en \Omega abiero y conexo vale la fórmula integral de Cauchy:
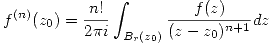
Aplicando módulos: 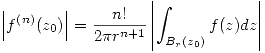
Ahora aplicando la desigualdad ML: 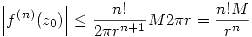
Parte c
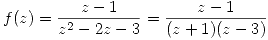
Tiene 2 polos simples (en 3 y en -1), por lo tanto si lo queremos desarrollar alrededor de  tendrá tres desarroollos en series de Laurent, uno en cada corona circular de centro
tendrá tres desarroollos en series de Laurent, uno en cada corona circular de centro  que no toque las singularidades.
que no toque las singularidades.
Si me piden el que converge en  , me están pidiendo el que converge en
, me están pidiendo el que converge en 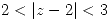 .
.
Haciendo fracciones simples llegamos a:
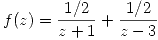 . Entonces puedo sacar la serie que converge a cada término y la función convergerá en la intersección de las regiones de convergencia.
. Entonces puedo sacar la serie que converge a cada término y la función convergerá en la intersección de las regiones de convergencia.
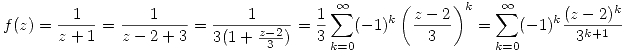 que converge cuando
que converge cuando 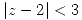
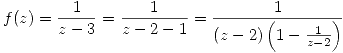
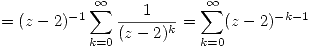 que converge cuando
que converge cuando 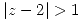
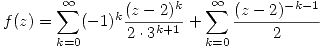
Para escribir la serie de Laurent consideramos entonces: 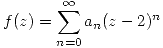 con
con