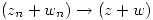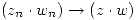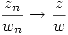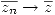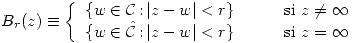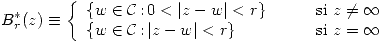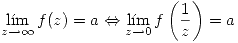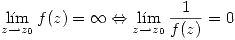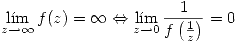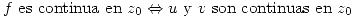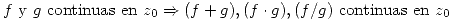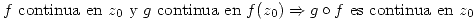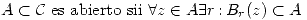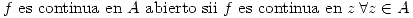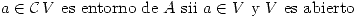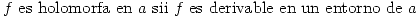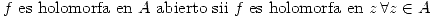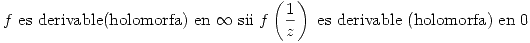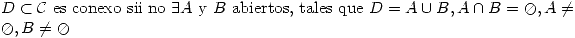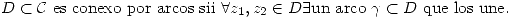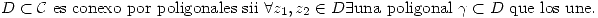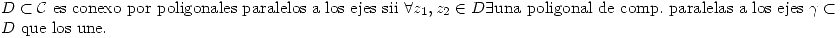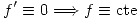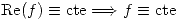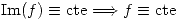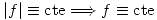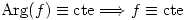Apunte Teórico de Análisis Matemático III B
Este apunte es para el curso de Gonzalez. (Turno de la mañana)
Unidad 1
Sucesiones
Definición: Límite de una sucesión. Sea 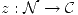
Diremos que 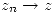 (o converge) sii
(o converge) sii 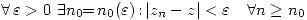
Si no converge diremos que diverge.
Propiedades: Sea 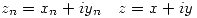
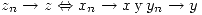
- Si
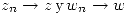
Definición: 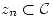 es acotada sii
es acotada sii 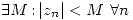
Proposición: 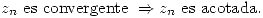
Funciones
Definiciones:
- Entornos en
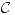 . Sea
. Sea 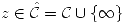 Se definen:
Se definen: - Límite de una función: Sean
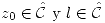 . Diremos que la función converge, o que
. Diremos que la función converge, o que 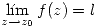 sii
sii 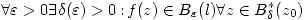
Propiedades: Sean 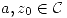
Continuidad
Definición: 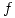 es continua en
es continua en 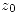 sii
sii 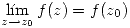
Propiedades: Sea 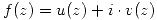 :
:
Definiciones:
Derivabilidad
Definición: Sea 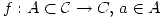
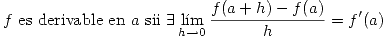
Proposición:
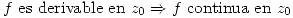
D) ![<tex> f(a+h)-f(a)=\left[ \frac{f(a+h)-f(a)}{h} \right]\cdot h \Rightarrow \lim_{h\rightarrow 0}f(a+h)-f(a)=0</tex> <tex> f(a+h)-f(a)=\left[ \frac{f(a+h)-f(a)}{h} \right]\cdot h \Rightarrow \lim_{h\rightarrow 0}f(a+h)-f(a)=0</tex>](lib/plugins/latex/images/4f52c43852d25047f50c164f553f99d396d3d017_0.png)
Definiciones:
Teorema de Cauchy-Riemann: Sea 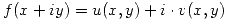 :
Si
:
Si 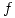 es derivable en
es derivable en 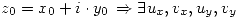 que verifican
que verifican 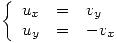 en
en 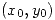 , y además
, y además 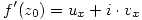
D) 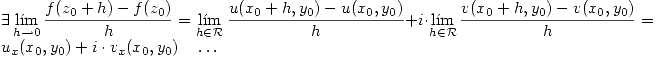
Observación:
- La recíproca del teorema se cumple si
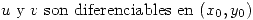
- Si
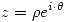 podemos escribir:
podemos escribir: 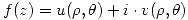 . Entonces podemos escribir las ecuaciones de Cauchy-Riemann como:
. Entonces podemos escribir las ecuaciones de Cauchy-Riemann como: 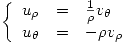
D)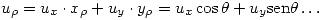
Conexidad
Observación: Si un conjunto es abierto las cuatro definiciones anteriores son equivalentes. Por lo tanto cuando se diga abierto y conexo se puede referir a cualquiera de las cuatro definiciones anteriores.
Proposición: Sea 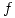 holomorfa en
holomorfa en 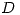 abierto y conexo. Entonces:
abierto y conexo. Entonces:
D)(del item 1)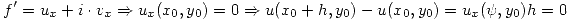 Entonces:
Entonces: 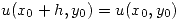 Se puede demostrar lo mismo para la segunda coordenada y para
Se puede demostrar lo mismo para la segunda coordenada y para  . Por lo tanto, usando el camino por poligonales, se demuestra que para cualquier par de puntos
. Por lo tanto, usando el camino por poligonales, se demuestra que para cualquier par de puntos 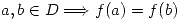 .
.
Unidad 2
Funciones elementales
Se definen las siguientes funciones elementales:
- Función exponencial
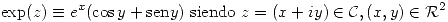
Con esta definición se cumple 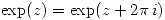 Se usará también
Se usará también 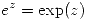
- Funciones trigonométricas
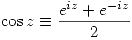 , y
, y 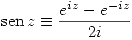
- Funciones hiperbólicas
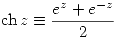 , y
, y 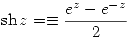
- Función logarítmica
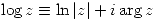 Es una función multiforme, pues la función argumento devuelve infinitos valores para el mismo número complejo.
Es una función multiforme, pues la función argumento devuelve infinitos valores para el mismo número complejo.
Definición: Dada una función multiforme  definida en
definida en 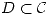 , una rama es una función (uniforme)
, una rama es una función (uniforme) 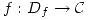 holomorfa en
holomorfa en 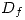 y
y 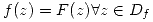
Por lo tanto si uno toma una rama de la función argumento, está tomando una rama del logaritmo. Si uno elige el argumento principal, está eligiendo la rama principal del logaritmo.
- Potencia compleja
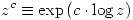 que también es una función multiforme.
que también es una función multiforme.
Transformaciones del plano: Homografía
Una homografía es una función 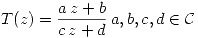 .
.
Cumplen la propiedad de ser composición de transformaciones elementales. Transforma rectas y circinferencias en rectas o circunferencias.
Teorema Dados 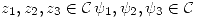 , existe una única homografía tal que
, existe una única homografía tal que 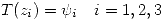 y se cumple que
y se cumple que 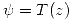 con:
con:
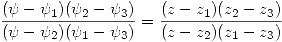
Definición: Se dice que una transformación es conforme en 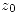 si para todo par de curvas que se intersecan en
si para todo par de curvas que se intersecan en 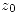 conserva el ángulo entre ellas (tanto en magnitud como en sentido).
conserva el ángulo entre ellas (tanto en magnitud como en sentido).
Observación: Si 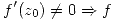 es conforme en
es conforme en 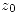 . La vuelta sólo es válida si
. La vuelta sólo es válida si 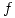 es derivable en
es derivable en 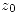 .
.
Unidad 3
Integración
Definición: Integral compleja de variable real Sea ![<tex> f:[a,b]\subset\mathcal{R}\rightarrow\mathcal{C} </tex> <tex> f:[a,b]\subset\mathcal{R}\rightarrow\mathcal{C} </tex>](lib/plugins/latex/images/6db9ea214c8ef587d1f0ff8c6a94c78fd782976a_0.png) se define:
se define: 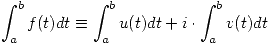
- Una curva de
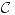 es un conjunto
es un conjunto ![<tex>\Gamma=\{ z\in\mathcal{C}:z(t)=x(t)+iy(t),t\in[a,b]\subset\mathcal{R},x,y\mbox{ cont. en }[a,b]\}</tex> <tex>\Gamma=\{ z\in\mathcal{C}:z(t)=x(t)+iy(t),t\in[a,b]\subset\mathcal{R},x,y\mbox{ cont. en }[a,b]\}</tex>](lib/plugins/latex/images/7a1c3083ff7261d2b7598bb162ff3fe6f273f343_0.png) . Se denomina
. Se denomina  puntos inicial y final de la curva respectivamente. La curva
puntos inicial y final de la curva respectivamente. La curva 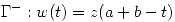 se denomina curva inversa.
se denomina curva inversa.
- Una curva se denomina cerrada sii
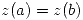 . Se denomina simple sii
. Se denomina simple sii 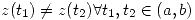
- Si
![<tex> x(t),y(t)\in\mathcal{C}_{[a,b]}^1 </tex> <tex> x(t),y(t)\in\mathcal{C}_{[a,b]}^1 </tex>](lib/plugins/latex/images/45063b4f4f06d0b9c638cf62d65e83a498e1ea71_0.png) se dice que
se dice que  es curva diferenciable (o arco diferenciable).
es curva diferenciable (o arco diferenciable).
- Si existe una partición
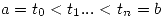 tal que
tal que ![<tex> \Gamma_{[t_i,t_{i+1}]} (i=0,...n-1) </tex> <tex> \Gamma_{[t_i,t_{i+1}]} (i=0,...n-1) </tex>](lib/plugins/latex/images/6fe1a9802ecca6ccf4e9a79255d8291bab81f97a_0.png) es curva diferenciable., se dice que
es curva diferenciable., se dice que 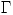 es una curva diferenciable a tramos o contorno.
es una curva diferenciable a tramos o contorno.
Definición: Integración de una función compleja.
- Sea
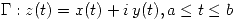 curva diferenciable,
curva diferenciable, 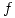 continua sobre
continua sobre 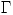 , se define:
, se define: 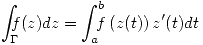
- Sea
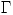 diferenciable a trozos, entonces
diferenciable a trozos, entonces ![<tex> \int_{\Gamma}\!\!\!\! f(z)dz = \sum_{i=0}^{n-1} \int_{\Gamma_i} \!\!\!\! f(z)dz \quad \Gamma_i=\Gamma_{[t_i,t_{i+1}]} </tex> <tex> \int_{\Gamma}\!\!\!\! f(z)dz = \sum_{i=0}^{n-1} \int_{\Gamma_i} \!\!\!\! f(z)dz \quad \Gamma_i=\Gamma_{[t_i,t_{i+1}]} </tex>](lib/plugins/latex/images/cb930b27a10774547c260012f299167302bcbc69_0.png)
Fórmula de mayoración:
Sea 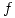 continua sobre
continua sobre 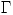 (contorno) y
(contorno) y 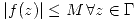 , entonces:
, entonces: 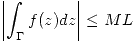 donde
donde 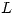 es la longitud de la curva.
es la longitud de la curva.
D) 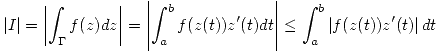
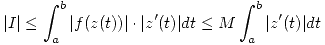
Definición: Sea 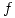 holomorfa en
holomorfa en  . Una función
. Una función 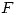 holomorfa en
holomorfa en  es una primitiva de
es una primitiva de 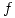 sii
sii 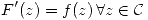 .
.
Prop: Dos primitivas de una misma 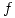 sobre un dominio
sobre un dominio  difieren en una constante. D) Supongamos que
difieren en una constante. D) Supongamos que 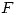 y
y 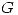 son primitivas de
son primitivas de 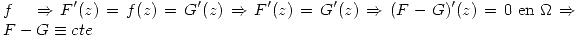
Teorema: (Regla de Barrow generalizada) Sea 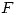 primitiva de
primitiva de 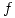 en
en  (dominio) y
(dominio) y 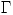 un controno de
un controno de  con punto inicial
con punto inicial 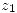 y punto final
y punto final 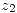 . Entonces:
. Entonces: 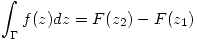 .
.
D) Sea ![<tex> \Gamma : z(t), t\in [ \alpha ,\beta ], z(\alpha)=z_1, z(\beta)=z_2 </tex> <tex> \Gamma : z(t), t\in [ \alpha ,\beta ], z(\alpha)=z_1, z(\beta)=z_2 </tex>](lib/plugins/latex/images/3f3adbcc3e0d26481b0f75c0514534e03cd72a37_0.png)
![<tex> \alpha=t_0<t_1... t_n=\beta \quad z(t)\in\mathcal{C}_{[t_i,t_{i+1}]}^1, i=0,1...(n-1)</tex> <tex> \alpha=t_0<t_1... t_n=\beta \quad z(t)\in\mathcal{C}_{[t_i,t_{i+1}]}^1, i=0,1...(n-1)</tex>](lib/plugins/latex/images/6445c4f989481d880c11be8c2bc5d76c61eff46e_0.png)
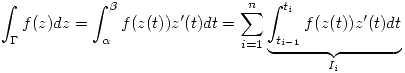
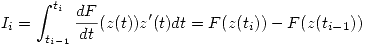 …
…
Definición: Un dominio  se dice simplemente conexo si todo contorno simple cerrado contenido en
se dice simplemente conexo si todo contorno simple cerrado contenido en  tiene en su interior sólo puntos de
tiene en su interior sólo puntos de  .
.
Teorema de Cauchy-Goursat Sea  abierto y conexo con
abierto y conexo con 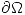 (curva) cerrada. Si
(curva) cerrada. Si 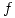 es holomorfa en
es holomorfa en  y continua sobre
y continua sobre 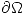 , entonces
, entonces 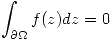 .
.
D) ![<tex> f=u+iv \quad \partial\Omega : z(t), t\in [ \alpha,\beta ] </tex> <tex> f=u+iv \quad \partial\Omega : z(t), t\in [ \alpha,\beta ] </tex>](lib/plugins/latex/images/db8f977390f5ef82ef7afeea019d36ec00669401_0.png) Entonces:
Entonces: ![<tex> I=\int_{\partial\Omega} f(z)dz=\int_{\alpha}^{\beta} \left[ u(x(t),y(t))+i\,v(x(t),y(t)) \right] \left( x'(t)+i\,y'(t) \right) dt= \int_{\alpha}^{\beta} \left[ u\,x'(t)-v\,y'(t) \right] dt + i \int_{\alpha}^{\beta} \left[ v\,x'(t)+u\,y'(t) \right] dt=\int_{\alpha}^{\beta} \left( udx-vdy \right)+i \int_{\alpha}^{\beta} \left( vdx+udy \right)=\int\!\!\!\!\int_{\Omega} (-v_x-u_y)dxdy+i \int\!\!\!\!\int_{\Omega} (u_x-v_y)dxdy =0 </tex> <tex> I=\int_{\partial\Omega} f(z)dz=\int_{\alpha}^{\beta} \left[ u(x(t),y(t))+i\,v(x(t),y(t)) \right] \left( x'(t)+i\,y'(t) \right) dt= \int_{\alpha}^{\beta} \left[ u\,x'(t)-v\,y'(t) \right] dt + i \int_{\alpha}^{\beta} \left[ v\,x'(t)+u\,y'(t) \right] dt=\int_{\alpha}^{\beta} \left( udx-vdy \right)+i \int_{\alpha}^{\beta} \left( vdx+udy \right)=\int\!\!\!\!\int_{\Omega} (-v_x-u_y)dxdy+i \int\!\!\!\!\int_{\Omega} (u_x-v_y)dxdy =0 </tex>](lib/plugins/latex/images/e7ec1b7a32f48161f0f7ac9b096cfd007bf3d70e_0.png)
En la penúltima igualdad se usó el Teorema de Green y en la última el de Cauchy-Riemann.