Analisis III Primer recuperatorio - 17 de junio de 2014
1. Analizar convergencia y calcular la integral 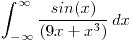
2. Resolver la ecuación del calor en estado estacionario en el recinto ![<tex>{(x,t) \in {\rm I\!R} ^2 : [0,\pi] \times [0,1]}</tex> <tex>{(x,t) \in {\rm I\!R} ^2 : [0,\pi] \times [0,1]}</tex>](lib/plugins/latex/images/95b74326f61e2b2748848c844f1cbed47b68b26b_0.png) con las condiciones de contorno del pizarrón.
con las condiciones de contorno del pizarrón.
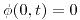
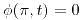


3. a) Hallar el desarrollo de Laurent en potencias de  :
: 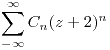 de la función
de la función 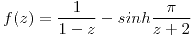 , de manera que la serie
, de manera que la serie 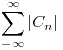 converja y calcular su suma. Dar el dominio de convergencia de dicho desarrollo.
b) ¿Qué tipo de singularidad tiene la función
converja y calcular su suma. Dar el dominio de convergencia de dicho desarrollo.
b) ¿Qué tipo de singularidad tiene la función  en
en 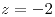 y cuánto vale su residuo?
y cuánto vale su residuo?
4. Hallar el desarrollo de Fourier de

Analizar la convergencia puntual 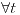 y calcular la suma
y calcular la suma 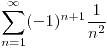
5. a) Es posible que la función 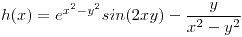 sea la parte real de una función analítica
sea la parte real de una función analítica 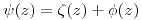 ? Justificar adecuadamente. b) Calcular
? Justificar adecuadamente. b) Calcular 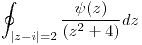
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
