Tabla de Contenidos
Primer Parcial 24/10/2006 - Cátedra Isaacson
Esta página está incompleta; podés ayudar completando el material.
Enunciado
- Utilizar la fórmula integral de Cauchy, para demostrar que:
 y
y 
- Dada
 ,
,  , determinar:
, determinar:- Para qué valores de
 , la serie de Laurent de
, la serie de Laurent de  tiene sólo términos de exponente no negativo y dar el radio de convergencia.
tiene sólo términos de exponente no negativo y dar el radio de convergencia. - Para qué valores de
 ,
,  es polo de
es polo de  de orden
de orden 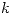 . Hallar en ese caso la serie de Laurent en un entonrno de
. Hallar en ese caso la serie de Laurent en un entonrno de  .
. - Analizar el comportamiento de
 en infinito y hallar, si existe, su correspondiente expansión en serie.
en infinito y hallar, si existe, su correspondiente expansión en serie.
- Hallar el desarrollo de Laurent de
 , válido en
, válido en  , considerando la determinación de
, considerando la determinación de  tal que
tal que  , definida en
, definida en  . Determinar
. Determinar  y
y ![<tex>Res[f(z), z=-1]</tex> <tex>Res[f(z), z=-1]</tex>](lib/plugins/latex/images/91417fe1187ad7ec1d23594935bd585a12fdca45_0.png) .
. - Hallar
 holomorfa salvo en
holomorfa salvo en  donde tenga polos simples, tal que
donde tenga polos simples, tal que ![<tex>Res[f(z), z=4]=-1</tex> <tex>Res[f(z), z=4]=-1</tex>](lib/plugins/latex/images/1c6ae2743ae412275cc98b6fd84b9c05a9d906c6_0.png) , tenga un cero de orden uno en infinito y
, tenga un cero de orden uno en infinito y  .
. - Analizar convergencia y calcular
 .
.
Resolución
Punto I
La clave de este ejercicio es darse cuenta que la integral ya está parametrizada. Para poder usar la Fórmula Integral de Cauchy hay que desparametrizar.
La parametrización es: 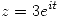 . Con lo cual,
. Con lo cual, 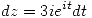 y
y 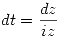 .
.
La primer integral ahora es
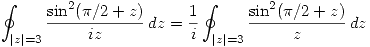 .
.
Como  es análitica sobre y en el interior de
es análitica sobre y en el interior de 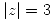 , por la Fórmula Integral de Cauchy:
, por la Fórmula Integral de Cauchy:
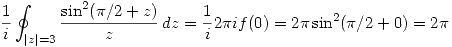 .
.
De la misma forma, para la otra integral se tiene:
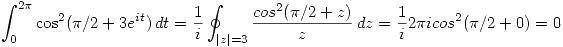 .
.
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
